题目内容
已知向量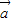 =(1,m),
=(1,m),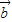 =(m,2),若
=(m,2),若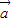 ∥
∥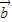 ,则实数m等于( )
,则实数m等于( )A.-
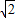
B.
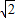
C.-
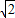 或
或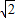
D.0
【答案】分析:直接利用向量共线的坐标表示列式进行计算.
解答:解:∵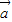 =(1,m),
=(1,m),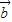 =(m,2),且
=(m,2),且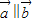 ,所以1•2=m•m,解得m=
,所以1•2=m•m,解得m=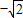 或m=
或m=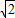 .
.
故选C.
点评:本题考查了平面向量的坐标运算,向量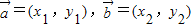 ,则
,则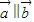 的充要条件是x1y2-x2y1=0,是基础题.
的充要条件是x1y2-x2y1=0,是基础题.
解答:解:∵
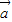 =(1,m),
=(1,m),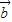 =(m,2),且
=(m,2),且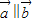 ,所以1•2=m•m,解得m=
,所以1•2=m•m,解得m=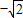 或m=
或m=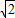 .
.故选C.
点评:本题考查了平面向量的坐标运算,向量
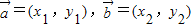 ,则
,则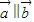 的充要条件是x1y2-x2y1=0,是基础题.
的充要条件是x1y2-x2y1=0,是基础题. 
练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
已知向量
=(1,-m),
=(m2,m),则向量
+
所在的直线可能为( )
| a |
| b |
| a |
| b |
| A、x轴 |
| B、第一、三象限的角平分线 |
| C、y轴 |
| D、第二、四象限的角平分线 |
已知向量
=(1,m),
=(2,n),
=(3,t),且
∥
,
⊥
,则|
|2+|
|2的最小值为( )
| a |
| b |
| c |
| a |
| b |
| b |
| c |
| a |
| c |
| A、20 | B、16 | C、10 | D、4 |