Question

如下图所示，已知Rt△ABC所在平面外一点S，且SA＝SB＝SC

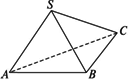
(1)求证：点S与斜边AC中点D的连线SD⊥面ABC；

(2)若直角边BA＝BC，求证：BD⊥面SAC

Answer 1

答案：
解析：

　　证明：(1)过S作SO⊥面ABC于O，∵SA＝SB＝SC，

　　∴O为△ABC的外心．

　　而△ABC为直角三角形，∴O为斜边AC的中点，即O与D点重合．

　　∴SD⊥面ABC．

　　(2)∵BA＝BC，∴BD⊥AC

　　又SD⊥面ABC，∴SD⊥BD，即BD⊥SD．SD∩AC＝D，

　　∴BD⊥面SAC

提示：

对于第(1)问可以先过S点作底面的垂线，再证垂足与O点重合即可．对于第(2)问，可利用第(1)问的结果，把线面垂直转化为线线垂直，即证BD⊥AC，BD⊥SD