题目内容
求函数f（x）=2x 3－3x+1零点的个数.
解析：先用计算机或计算器作出f（x）的对应值表，然后根据函数零点的判定方法来判定函数的零点.
解： 用计算器或计算机作出x、f（x）的对应值表（如下表）和图象（如下图).
X | -1.5 | -1 | -0.5 | 0 | 0.5 | 1 | 1.5 |
F(x) | -1.25 | 2 | 2.25 | 1 | -0.25 | 0 | 3.25 |
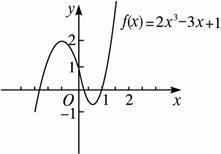
由上表和上图可知，f（－1.5）＜0，f（－1）＞0，即f（－1.5）·f（－1）＜0，说明这个函数在区间（－1.5，－1）内有零点.同理，它在区间（0，0.5）内也有零点.另外，f（1）=0，所以1也是它的零点.由于函数f（x）在定义域（－∞，－1.5）和（1，+∞）内是增函数，所以它共有3个零点.
练习册系列答案
冲刺100分1号卷系列答案
相关题目
（2012•湖南模拟）选做题（请考生在第16题的三个小题中任选两题作答，如果全做，则按前两题记分，要写出必要的推理与演算过程）