题目内容
已知函数![]() ,其中
,其中![]()
(1)求函数![]() 在
在![]() 是减函数的充要条件;
是减函数的充要条件;
(2)求函数![]() 在
在![]() 的最大值;
的最大值;
(3)解不等式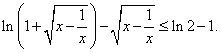
【解】(1)![]()
因为![]()
所以当![]() 时,
时,![]() ,即
,即![]()
当![]() 时,因为
时,因为![]() ,所以
,所以![]() 即
即![]()
故![]() 在
在![]() 是减函数的充要条件是
是减函数的充要条件是![]() 4分
4分
(2)由(1)知,当![]() 时
时![]() 在
在![]() 是减函数,此时
是减函数,此时![]()
当![]() 时,令
时,令![]() 得
得![]() ,
,
于是![]() 在
在![]() 上单增,在
上单增,在![]() 上单减,
上单减,
![]()
综上可知: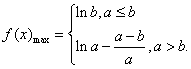 8分
8分
(3)在(1)中取![]() 即
即![]()
由(1)知![]() 在
在![]() 是减函数
是减函数
因为不等式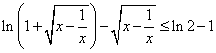 等价于
等价于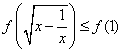
所以![]() ,解得
,解得![]() 或
或![]() ,
,
故原不等式的解集为:![]() 或
或![]() 12分
12分

练习册系列答案
相关题目
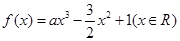 ,其中
,其中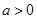 .
.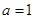 ,求曲线
,求曲线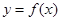 在点
在点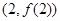 处的切线方程;
处的切线方程;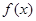 有三个零点,求
有三个零点,求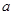 的取值范围.
的取值范围.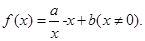 ,其中
,其中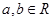
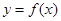 在点
在点 处的切线方程为
处的切线方程为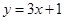 ,求函数
,求函数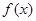 的解析式;
的解析式;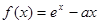 ,其中
,其中 .
. 恒成立,求
恒成立,求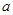 的取值范围;
的取值范围; 的图像上取定两点
的图像上取定两点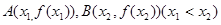 ,记直线
,记直线 的斜率为
的斜率为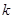 ,证明:存在
,证明:存在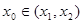 ,使
,使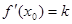 成立.
成立.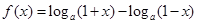 ,其中
,其中 .
.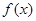 的定义域;
的定义域;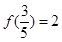 ,求使
,求使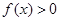 成立的
成立的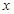 的集合。
的集合。