题目内容
【题目】已知函数![]() (
(![]() ).
).
(1)若![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 垂直,求实数
垂直,求实数![]() 的值;
的值;
(2)求函数![]() 的单调区间;
的单调区间;
(3)讨论函数![]() 在区间
在区间![]() 上零点的个数.
上零点的个数.
【答案】(1)![]() (2)见解析(3)见解析
(2)见解析(3)见解析
【解析】试题分析:由![]()
![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,
,
所以![]() 得出a值,(2)确定函数的单调区间
得出a值,(2)确定函数的单调区间![]()
![]() 大于零或小于零解不等式即可注意当当
大于零或小于零解不等式即可注意当当![]() ,
, ![]() 时(3)由(2)可知,
时(3)由(2)可知,
当![]() 时,
时, ![]() 在
在![]() 上单调递增,而
上单调递增,而![]() ,故
,故![]() 在
在![]() 上没有零点;
上没有零点;
当![]() 时,
时, ![]() 在
在![]() 上单调递增,而
上单调递增,而![]() ,故
,故![]() 在
在![]() 上有一个零点;只需讨论当
上有一个零点;只需讨论当![]() 时结合草图根据零点所在的区间逐一讨论即可
时结合草图根据零点所在的区间逐一讨论即可
试题解析:
(1)由题可知![]() 的定义域为
的定义域为![]() ,
,
因为![]() ,所以
,所以![]()
![]()
又因为直线![]() 的斜率为
的斜率为![]() ,
,
![]() ,解得
,解得![]()
(2)由(1)知: ![]()
![]() ,
,
当![]() 时,
时, ![]() ,所以
,所以![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,由
时,由![]() 得
得![]() ,由
,由![]() 得
得![]() ,所以
,所以![]() 在
在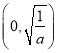 上单调递增,在
上单调递增,在 上单调递减.
上单调递减.
综上所述:当![]() 时,
时, ![]() 在
在![]() 上单调递增;当
上单调递增;当![]() 时,
时, ![]() 在
在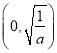 上单调递增,在
上单调递增,在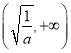 上单调递减.
上单调递减.
(3)由(2)可知,
当![]() 时,
时, ![]() 在
在![]() 上单调递增,而
上单调递增,而![]() ,故
,故![]() 在
在![]() 上没有零点;
上没有零点;
当![]() 时,
时, ![]() 在
在![]() 上单调递增,而
上单调递增,而![]() ,故
,故![]() 在
在![]() 上有一个零点;
上有一个零点;
当![]() 时,
时,
①若![]() ,即
,即![]() 时,
时, ![]() 在
在![]() 上单调递减,
上单调递减, ![]() ,
, ![]() 在
在![]() 上没有零点;
上没有零点;
②若![]() ,即
,即![]() 时,
时, ![]() 在
在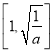 上单调递增,在
上单调递增,在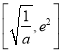 上单调递减,而
上单调递减,而![]() ,
, 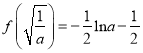 ,
, ![]() ,
,
若
![]() ,即
,即![]() 时,
时, ![]() 在
在![]() 上没有零点;
上没有零点;
若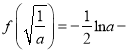
![]() ,即
,即![]() 时,
时, ![]() 在
在![]() 上有一个零点;
上有一个零点;
若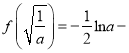
![]() ,即
,即![]() 时,由
时,由![]() 得
得![]() ,此时,
,此时, ![]() 在
在![]() 上有一个零点;
上有一个零点;
由![]() 得
得![]() ,此时,
,此时, ![]() 在
在![]() 上有两个零点;
上有两个零点;
③若![]() ,即
,即![]() 时,
时, ![]() 在
在![]() 上单调递增,
上单调递增, ![]() ,
, ![]() ,
, ![]() 在
在![]() 上有一个零点.
上有一个零点.
综上所述:当![]() 或
或![]() 时,
时, ![]() 在
在![]() 上有一个零点;当
上有一个零点;当![]() 或
或![]() 时,
时, ![]() 在
在![]() 上没有零点;当
上没有零点;当![]() 时,
时, ![]() 在
在![]() 上有两个零点.
上有两个零点.

 习题精选系列答案
习题精选系列答案【题目】某农场计划种植某种新作物,为此对这种作物的两个品种(分别称为品种甲和品种乙)进行田间试验.选取两大块地,每大块地分成![]() 小块地,在总共
小块地,在总共![]() 小块地中,随机选
小块地中,随机选![]() 小块地种植品种甲,另外
小块地种植品种甲,另外![]() 小块地种植品种乙.
小块地种植品种乙.
(1)假设![]() ,求第一大块地都种植品种甲的概率;
,求第一大块地都种植品种甲的概率;
(2)试验时每大块地分成![]() 小块,即
小块,即![]() ,试验结束后得到品种甲和品种乙在各小块地上的每公顷产量(单位:kg/hm2)如下表:
,试验结束后得到品种甲和品种乙在各小块地上的每公顷产量(单位:kg/hm2)如下表:
甲 |
|
|
|
|
|
|
|
|
乙 |
|
|
|
|
|
|
|
|
分别求品种甲和品种乙的每公顷产量的样本平均数和样本方差;根据试验结果,你认为应该种植哪一品种?
【题目】在测试中,客观题难度的计算公式为![]() ,其中
,其中![]() 为第
为第![]() 题的难度,
题的难度, ![]() 为答对该题的人数,
为答对该题的人数, ![]() 为参加测试的总人数.现对某校高三年级240名学生进行一次测试,共5道客观题,测试前根据对学生的了解,预估了每道题的难度,如表所示:
为参加测试的总人数.现对某校高三年级240名学生进行一次测试,共5道客观题,测试前根据对学生的了解,预估了每道题的难度,如表所示:
题号 | 1 | 2 | 3 | 4 | 5 |
考前预估难度 | 0.9 | 0.8 | 0.7 | 0.6 | 0.4 |
测试后,从中随机抽取了20名学生的答题数据进行统计,结果如表:

(Ⅰ)根据题中数据,估计中240名学生中第5题的实测答对人数;
(Ⅱ)从抽样的20名学生中随机抽取2名学生,记这2名学生中第5题答对的人数为![]() ,求
,求![]() 的分布列和数学期望;
的分布列和数学期望;
(Ⅲ)试题的预估难度和实测难度之间会有偏差.设![]() 为第
为第![]() 题的实测难度,请用
题的实测难度,请用![]() 和
和![]() 设计一个统计量,并制定一个标准来判断本次测试对难度的预估是否合理.
设计一个统计量,并制定一个标准来判断本次测试对难度的预估是否合理.