题目内容
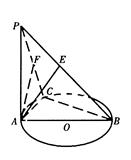
(本小题满分13分)在四棱锥 中,底面
中,底面 是菱形,
是菱形, .
.
(Ⅰ)若 ,求证:
,求证: 平面
平面 ;
;
(Ⅱ)若平面 平
平 面
面 ,求证:
,求证: ;
;
(Ⅲ)在棱 上是否存在点
上是否存在点 (异于点
(异于点 )使得
)使得 ∥平面
∥平面 ,若存在,求
,若存在,求 的值;若不存在,说明理由.
的值;若不存在,说明理由.

 中,底面
中,底面 是菱形,
是菱形, .
.(Ⅰ)若
 ,求证:
,求证: 平面
平面 ;
;(Ⅱ)若平面
 平
平 面
面 ,求证:
,求证: ;
;(Ⅲ)在棱
 上是否存在点
上是否存在点 (异于点
(异于点 )使得
)使得 ∥平面
∥平面 ,若存在,求
,若存在,求 的值;若不存在,说明理由.
的值;若不存在,说明理由.
(17)(本小题满分14分)

(Ⅰ)证明:因为 底面 是菱形
是菱形
所以 . ………………………………………1分
. ………………………………………1分
因为 ,
, ,
,
所以 平面
平面 . ………………………………………3分
. ………………………………………3分
(Ⅱ)证明:由(Ⅰ)可知 .
.
因为平面 平面
平面
 ,平面
,平面 平面
平面 ,
,
 平面
平面 ,
,
所以 平面
平面 . ………………………………………5分
. ………………………………………5分
因为 平面
平面 ,
,
所以 . ……………………………7分
. ……………………………7分
因为 底面 是菱形,
是菱形,
所以 .
.
所以 . ………………………………………8分
. ………………………………………8分
(Ⅲ)解:不存在. 下面用反证法说明. ………………………………………9分
假设存在点 (异于点
(异于点 )使得
)使得
 ∥平面
∥平面 .
.
在菱形 中,
中, ∥
∥ ,
,
因为 平面
平面 ,
, 平面
平面 ,
,
所以 ∥平面
∥平面 .
.
………………………………………11分
因为 平面
平面 ,
, 平面
平面 ,
,
 ,
,
所以 平面 ∥平面
∥平面
 .
.
………………………………………13分
而平面 与平面
与平面 相交,矛盾. ………………………………………14分
相交,矛盾. ………………………………………14分

(Ⅰ)证明:因为 底面
 是菱形
是菱形所以
 . ………………………………………1分
. ………………………………………1分因为
 ,
, ,
,所以
 平面
平面 . ………………………………………3分
. ………………………………………3分(Ⅱ)证明:由(Ⅰ)可知
 .
.因为平面
 平面
平面
 ,平面
,平面 平面
平面 ,
, 平面
平面 ,
,所以
 平面
平面 . ………………………………………5分
. ………………………………………5分因为
 平面
平面 ,
,所以
 . ……………………………7分
. ……………………………7分因为 底面
 是菱形,
是菱形,所以
 .
. 所以
 . ………………………………………8分
. ………………………………………8分(Ⅲ)解:不存在. 下面用反证法说明. ………………………………………9分
假设存在点
 (异于点
(异于点 )使得
)使得
 ∥平面
∥平面 .
.在菱形
 中,
中, ∥
∥ ,
,因为
 平面
平面 ,
, 平面
平面 ,
,所以
 ∥平面
∥平面 .
. ………………………………………11分
因为
 平面
平面 ,
, 平面
平面 ,
, ,
,所以 平面
 ∥平面
∥平面
 .
. ………………………………………13分
而平面
 与平面
与平面 相交,矛盾. ………………………………………14分
相交,矛盾. ………………………………………14分略

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
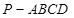 中,底面
中,底面 为菱形,
为菱形, ,
, 为
为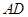 的中点,
的中点,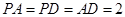 .
.
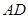
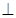 平面
平面 ;
;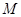 在线段
在线段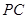 上,
上,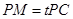 ,试确定
,试确定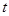 的值,使
的值,使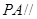 平面
平面 ;
;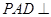 平面
平面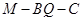 的大小.
的大小. 中,四边形
中,四边形 为平行四边形,且面
为平行四边形,且面 面
面 ,
,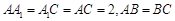 ,且
,且 ,
, 为
为 中点.
中点. 平面
平面 与平面
与平面 所成角的正弦值.
所成角的正弦值.
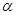 和直线
和直线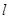 ,
,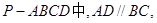
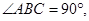
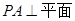
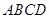 ,
,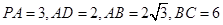 ,
, 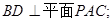
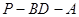 的大小.
的大小.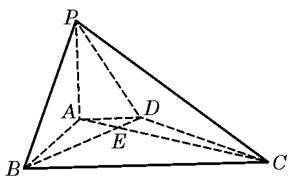
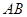 是⊙O的直径,C是圆周上不同于A、B的点,PA垂直于⊙O所在平面
是⊙O的直径,C是圆周上不同于A、B的点,PA垂直于⊙O所在平面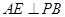 于E,
于E,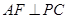 于F,因此________⊥平面PBC(请填图上的一条直线)
于F,因此________⊥平面PBC(请填图上的一条直线)