题目内容
2.试在14和224之间插入3个数,使5个数成等比数列,求这三个数.分析 根据这五个数成等比数列,先求出公比,再分类讨论求得中间三项.
解答 解:设a1=14,a5=224,
因为这五个数成等比数列,设公比为q,
所以,a1q4=a5,
所以,q4=$\frac{224}{14}$=16,
解得q=2或q=-2,
①当q=2时,插入的这三个数分别为:28,56,112;
②当q=-2时,插入的这三个数分别为:-28,56,-112;
因此,插入的这三个数分别为:28,56,112或:-28,56,-112.
点评 本题主要考查了等比数列的通项公式,涉及分类讨论解题思想,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.下列命题中不正确的是( )
| A. | 向量$\overrightarrow{AB}$与向量$\overrightarrow{BA}$的长度相等 | |
| B. | 任意一个非零向量都可以平行移动 | |
| C. | 若$\overrightarrow{a}$∥$\overrightarrow{b}$,且$\overrightarrow{b}$≠$\overrightarrow{0}$,则$\overrightarrow{a}$≠$\overrightarrow{0}$ | |
| D. | 两个有共同起点且共线的向量,其终点不一定相同. |
7.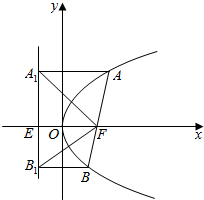 如图所示,线段AB时抛物线的焦点弦,F为抛物线焦点,若A,B在其准线上的射影分别为A1,B1,则∠A1FB1等于( )
如图所示,线段AB时抛物线的焦点弦,F为抛物线焦点,若A,B在其准线上的射影分别为A1,B1,则∠A1FB1等于( )
 如图所示,线段AB时抛物线的焦点弦,F为抛物线焦点,若A,B在其准线上的射影分别为A1,B1,则∠A1FB1等于( )
如图所示,线段AB时抛物线的焦点弦,F为抛物线焦点,若A,B在其准线上的射影分别为A1,B1,则∠A1FB1等于( )| A. | 45° | B. | 60° | C. | 90° | D. | 120° |