Question

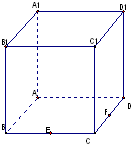单位正方体ABCD-A₁B₁C₁D₁中，E，F分别是BC，CD中点，平面A₁EF交BB₁于M，交DD₁于N
（1）画出几何体A₁MEFN-ABEFD的直观图与三视图；
（2）设AC中点为O，在CC₁上寻找一点G，使OG⊥平面A₁EF，求CG的长．

Answer 1

分析：（1）几何体A₁MEFN-ABEFD的直观图与三视图如图（1、2）．
（2）设AC交EF于S，若OG⊥平面A₁EF，则OG⊥A₁S，根据

GC

OC

=tan∠GOC=

1

tan∠A1SA

=

AS

AA1

，可得CG=

OC×AS

AA1

，
运算求得结果．

解答：解：（1）直观图与三视图如图（1、2）

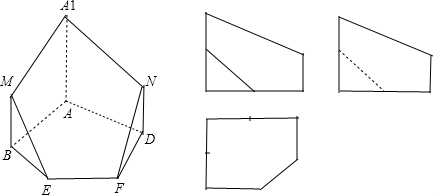
           图 1                              图 2  
 
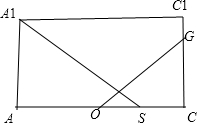
        图三
（2）设AC交EF于S，若OG⊥平面A₁EF，则OG⊥A₁S，如图3，
∵

GC

OC

=tan∠GOC=

1

tan∠A1SA

=

AS

AA1

，设正方体的棱长为1，∴CG=

OC×AS

AA1

=

2 2 × 3 2 4

1

=

3

4

．

点评：本题考查简单空间几何体的三视图，直线与平面垂直的判定，体现了数形结合的数学思想，是一道中档题．