题目内容
18.若目标函数z=x+y+1在约束条件$\left\{\begin{array}{l}{x+y-2≤0}\\{x-y+2≤0}\\{y≤n}\\{x≥-3}\end{array}\right.$下取得最大值时的最优解有无数多个,则n∈($\frac{1}{2}$,+∞).分析 画出约束条件表示的可行域,利用已知条件求出n的范围即可.
解答 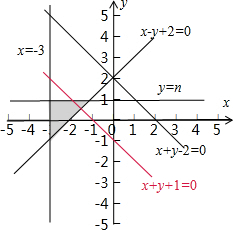 解:约束条件$\left\{\begin{array}{l}{x+y-2≤0}\\{x-y+2≤0}\\{y≤n}\\{x≥-3}\end{array}\right.$表示的可行域如图
解:约束条件$\left\{\begin{array}{l}{x+y-2≤0}\\{x-y+2≤0}\\{y≤n}\\{x≥-3}\end{array}\right.$表示的可行域如图
目标函数z=x+y+1在约束条件$\left\{\begin{array}{l}{x+y-2≤0}\\{x-y+2≤0}\\{y≤n}\\{x≥-3}\end{array}\right.$下取得最大值时的最优解有无数多个,可行域内x+y+1=0有线段在阴影部分,
由$\left\{\begin{array}{l}{x-y+2=0}\\{x+y+1=0}\end{array}\right.$,解得y=$\frac{1}{2}$
则:n>$\frac{1}{2}$,
即:n∈($\frac{1}{2}$,+∞).
点评 本题考查线性规划的应用,解题的关键是可行域以及最优解有无数个的理解,考查计算能力.

练习册系列答案
相关题目
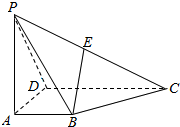 如图所示,四棱锥P-ABCD的底面是一梯形,AB∥CD,CD=3AB,过点B作平面PAD的平行线交直线PC于点E,则点PE:EC=1:2.
如图所示,四棱锥P-ABCD的底面是一梯形,AB∥CD,CD=3AB,过点B作平面PAD的平行线交直线PC于点E,则点PE:EC=1:2.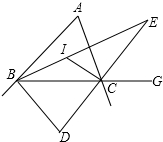 好学的小红在学完三角形的角平分线后,遇到下列4个问题,请你帮她解决,如图,在ABC中,∠BAC=50°,点I是两角B、C平分线的交点.
好学的小红在学完三角形的角平分线后,遇到下列4个问题,请你帮她解决,如图,在ABC中,∠BAC=50°,点I是两角B、C平分线的交点.