题目内容
【题目】2020年寒假期间新冠肺炎肆虐,全国人民众志成城抗击疫情.某市要求全体市民在家隔离,同时决定全市所有学校推迟开学.某区教育局为了让学生“停课不停学”,要求学校各科老师每天在网上授课,每天共280分钟,请学生自主学习.区教育局为了了解高三学生网上学习情况,上课几天后在全区高三学生中采取随机抽样的方法抽取了100名学生进行问卷调查,为了方便表述把学习时间在![]() 分钟的学生称为
分钟的学生称为![]() 类,把学习时间在
类,把学习时间在![]() 分钟的学生称为
分钟的学生称为![]() 类,把学习时间在
类,把学习时间在![]() 分钟的学生称为
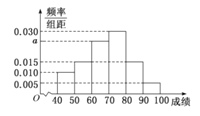
分钟的学生称为![]() 类,随机调查的100名学生学习时间的人数频率分布直方图如图所示:以频率估计概率回答下列问题:
类,随机调查的100名学生学习时间的人数频率分布直方图如图所示:以频率估计概率回答下列问题:

(1)求100名学生中![]() ,
,![]() ,
,![]() 三类学生分别有多少人?
三类学生分别有多少人?
(2)在![]() ,
,![]() ,
,![]() 三类学生中,按分层抽样的方法从上述100个学生中抽取10人,并在这10人中任意邀请3人电话访谈,求邀请的3人中是
三类学生中,按分层抽样的方法从上述100个学生中抽取10人,并在这10人中任意邀请3人电话访谈,求邀请的3人中是![]() 类的学生人数的分布列和数学期望;
类的学生人数的分布列和数学期望;
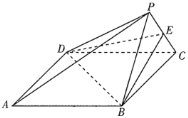
(3)某校高三(1)班有50名学生,某天语文和数学老师计划分别在19:00—19:40和20:00—20:40在线上与学生交流,由于受校园网络平台的限制,每次只能30个人同时在线学习交流.假设这两个时间段高三(1)班都有30名学生相互独立地随机登录参加学习交流.设![]() 表示参加语文或数学学习交流的人数,当
表示参加语文或数学学习交流的人数,当![]() 为多少时,其概率最大.
为多少时,其概率最大.
【答案】(1)30;(2)分布列见解析,![]() ;(3)42.
;(3)42.
【解析】
(1)根据频率分布直方图即可求出结果;
(2)根据分层抽样可知从![]() 类中抽2人,
类中抽2人,![]() 类中抽5人,
类中抽5人,![]() 类中抽3人,再根据超几何分布列出分布列,求出期望;
类中抽3人,再根据超几何分布列出分布列,求出期望;
(3)学生随机独立参加语文或数学在线辅导所包含的基本事件总数为![]() ,当
,当![]() 时,由韦恩图可知,事件
时,由韦恩图可知,事件![]() 所包含的基本事件的总数为
所包含的基本事件的总数为![]() ,
,
所以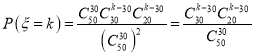 最大,列出不等式组,可得
最大,列出不等式组,可得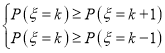 ,由此即可求出结果.
,由此即可求出结果.
(1)![]() 类学生有:
类学生有:![]() 人,
人,
![]() 类学生有:
类学生有:![]() 人,
人,
![]() 类学生有:
类学生有:![]() 人.
人.
(2)![]() ,
,
故从![]() 类中抽2人,
类中抽2人,![]() 类中抽5人,
类中抽5人,![]() 类中抽3人.
类中抽3人.
设邀请的三人中是![]() 类的学生人数为
类的学生人数为![]() ,则
,则![]() 可取0,1,2,3.
可取0,1,2,3.
![]() ,
,![]() ,
,![]() ,
,![]() .
.
所以![]() 的分布列为
的分布列为
| 0 | 1 | 2 | 3 |
|
|
|
|
|
所以![]() .
.
(3)学生随机独立参加语文或数学在线辅导所包含的基本事件总数为![]() ,
,
当![]() 时,由韦恩图可知,只参加语文辅导的人数为
时,由韦恩图可知,只参加语文辅导的人数为![]() ,
,
只参加数学辅导的人数为![]() ,
,
语文和数学都参加辅导的人数为![]() .
.
事件![]() 所包含的基本事件的总数为
所包含的基本事件的总数为![]() ,
,
所以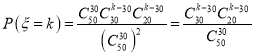 最大.
最大.
则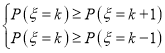 ,
,
所以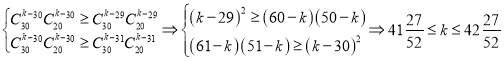 .
.
又因为![]() ,所以
,所以![]() .
.


【题目】已知某快递公司收取快递费的标准是:重量不超过![]() 的包裹收费
的包裹收费![]() 元;重量超过
元;重量超过![]() 的包裹,在收费
的包裹,在收费![]() 元的基础上,每超过
元的基础上,每超过![]() (不足
(不足![]() ,按
,按![]() 计算)需再收
计算)需再收![]() 元.该快递公司承揽了一个工艺品厂家的全部玻璃工艺品包裹的邮寄事宜,该厂家随机统计了
元.该快递公司承揽了一个工艺品厂家的全部玻璃工艺品包裹的邮寄事宜,该厂家随机统计了![]() 件这种包裹的两个统计数表如下:
件这种包裹的两个统计数表如下:
表![]()
包裹重量 |
|
|
|
|
|
包裹数 |
|
|
|
|
|
损坏件数 |
|
|
|
|
|
表![]()
包裹重量 |
|
|
|
|
|
出厂价(元 |
|
|
|
|
|
卖价(元 |
|
|
|
|
|
![]() 估计该快递公司对每件包裹收取快递费的平均值;
估计该快递公司对每件包裹收取快递费的平均值;
![]() 将包裹重量落入各组的频率视为概率,该工艺品厂家承担全部运费,每个包裹只有一件产品,如果客户收到有损坏品的包裹,该快递公司每件按其出厂价的
将包裹重量落入各组的频率视为概率,该工艺品厂家承担全部运费,每个包裹只有一件产品,如果客户收到有损坏品的包裹,该快递公司每件按其出厂价的![]() 赔偿给厂家.现该厂准备给客户邮寄重量在区间
赔偿给厂家.现该厂准备给客户邮寄重量在区间![]() 和
和![]() 内的工艺品各
内的工艺品各![]() 件,求该厂家这两件工艺品获得利润的分布列和期望.
件,求该厂家这两件工艺品获得利润的分布列和期望.