题目内容
【题目】若点![]() 为点
为点![]() 在平面
在平面![]() 上的正投影,则记
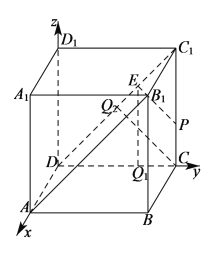
上的正投影,则记![]() .如图,在棱长为
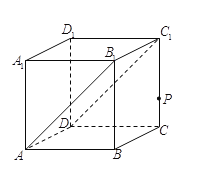
.如图,在棱长为![]() 的正方体
的正方体![]() 中,记平面
中,记平面![]() 为
为![]() ,平面
,平面![]() 为
为![]() ,点
,点![]() 是棱
是棱![]() 上一动点(与
上一动点(与![]() 、
、![]() 不重合)
不重合)![]() ,
,![]() .给出下列三个结论:
.给出下列三个结论:
①线段![]() 长度的取值范围是
长度的取值范围是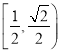 ;
;
②存在点![]() 使得
使得![]() 平面
平面![]() ;
;
③存在点![]() 使得
使得![]() .
.
其中,所有正确结论的序号是( )
A.①②③B.②③C.①③D.①②
【答案】D
【解析】
以点![]() 为坐标原点,
为坐标原点,![]() 、
、![]() 、
、![]() 所在直线分别为
所在直线分别为![]() 轴、
轴、![]() 轴、
轴、![]() 轴建立空间直角坐标系
轴建立空间直角坐标系![]() ,设点
,设点![]() 的坐标为
的坐标为![]() ,求出点
,求出点![]() 、
、![]() 的坐标,然后利用向量法来判断出命题①②③的正误.
的坐标,然后利用向量法来判断出命题①②③的正误.
取![]() 的中点
的中点![]() ,过点
,过点![]() 在平面
在平面![]() 内作
内作![]() ,再过点
,再过点![]() 在平面
在平面![]() 内作
内作![]() ,垂足为点
,垂足为点![]() .
.
在正方体![]() 中,
中,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,
又![]() ,
,![]() ,
,![]() 平面
平面![]() ,即
,即![]() ,
,![]() ,
,
同理可证![]() ,
,![]() ,则
,则![]() ,
,![]() .
.
以点![]() 为坐标原点,
为坐标原点,![]() 、
、![]() 、
、![]() 所在直线分别为
所在直线分别为![]() 轴、
轴、![]() 轴、
轴、![]() 轴建立空间直角坐标系
轴建立空间直角坐标系![]() ,设
,设![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
对于命题①,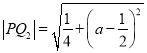 ,
,![]() ,则
,则![]() ,则
,则![]() ,所以,
,所以,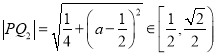 ,命题①正确;
,命题①正确;
对于命题②,![]() ,则平面
,则平面![]() 的一个法向量为
的一个法向量为![]() ,
,
![]() ,令
,令![]() ,解得
,解得![]() ,
,
所以,存在点![]() 使得
使得![]() 平面
平面![]() ,命题②正确;
,命题②正确;
对于命题③,![]() ,令
,令![]() ,
,
整理得![]() ,该方程无解,所以,不存在点
,该方程无解,所以,不存在点![]() 使得
使得![]() ,命题③错误.
,命题③错误.
故选:D.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目