题目内容
【题目】如图,点F1 , F2分别是椭圆C:![]() 的左、右焦点.点A是椭圆C上一点,点B是直线AF2与椭圆C的另一交点,且满足AF1⊥x轴,∠AF2F1=30°.
的左、右焦点.点A是椭圆C上一点,点B是直线AF2与椭圆C的另一交点,且满足AF1⊥x轴,∠AF2F1=30°.
(1)求椭圆C的离心率e;
(2)若△ABF1的周长为4![]() , 求椭圆C的标准方程;
, 求椭圆C的标准方程;
(3)若△ABF1的面积为8![]() , 求椭圆C的标准方程.
, 求椭圆C的标准方程.
【答案】解:(1)Rt△AF1F2中,∵∠AF2F1=30°,
∴![]() ,
,
则![]() ,代入
,代入![]() 并利用b2=a2﹣c2化简整理,
并利用b2=a2﹣c2化简整理,
得3a4﹣2a2c2﹣3c4=0,即(a2﹣3c2)(3a2﹣c2)=0,
∵a>c,
∴a=![]() c,
c,
∴e=![]() =
=![]() .
.
(2)由椭圆定义知AF1+AF2=BF1+BF2=2a,
∴△ABF1的周长为4a,
∴4a=4![]() ,则a=
,则a=![]() ,b=
,b=![]() ,
,
故椭圆C的标准方程为![]() ;
;
(3)由(1)知a=![]() c,则b=
c,则b=![]() c,
c,
于是椭圆方程可化为![]() ,即2x2+3y2=6c2 ,
,即2x2+3y2=6c2 ,
设直线AF2的方程为y=![]() (x-c),代入2x2+3y2=6c2化简整理得3x2﹣2cx﹣5c2=0,
(x-c),代入2x2+3y2=6c2化简整理得3x2﹣2cx﹣5c2=0,
∴x=﹣c或x=![]() c,
c,
则点B的横坐标为![]() c,
c,
∴点B到直线AF1的距离为![]() c-(-c)=
c-(-c)=![]() c
c
∴△ABF1的面积为![]() ,
,
解得c=3,
∴a=3![]() ,b=3
,b=3![]()
故椭圆C的标准方程为![]() .
.
【解析】(1)通过求解直角三角形得到A的坐标,代入椭圆方程整理,结合隐含条件求得椭圆C的离心率e;
(2)通过椭圆定义结合三角形的周长及隐含条件求得答案;
(3)由(1)得到a与c,b与c的关系,设直线AF2的方程为y=![]() (x-c),代入2x2+3y2=6c2化简整理,求得B的坐标,再由点到直线的距离公式结合三角形面积求得答案.
(x-c),代入2x2+3y2=6c2化简整理,求得B的坐标,再由点到直线的距离公式结合三角形面积求得答案.
【考点精析】本题主要考查了椭圆的标准方程的相关知识点,需要掌握椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() 才能正确解答此题.
才能正确解答此题.

【题目】某工科院校对![]() ,
, ![]() 两个专业的男女生人数进行调查,得到如下的列联表:
两个专业的男女生人数进行调查,得到如下的列联表:
专业 | 专业 | 总计 | |
女生 | 12 | 4 | 16 |
男生 | 38 | 46 | 84 |
总计 | 50 | 50 | 100 |
(Ⅰ)从![]() 专业的女生中随机抽取2名女生参加某项活动,其中女生甲被选到的概率是多少?
专业的女生中随机抽取2名女生参加某项活动,其中女生甲被选到的概率是多少?
(Ⅱ)能否有95%的把握认为工科院校中“性别”与“专业”有关系?
附: 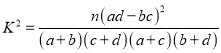 .
.
|
|
|
|
|
|
|
|
|
|
|
|