题目内容
一个车间为了规定工时定额,需要确定加工零件所花费的时间,为此进行了10次试验,测得数据如下:零件数x个 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
加工时间y分 | 62 | 68 | 75 | 81 | 89 | 95 | 102 | 108 | 115 | 122 |
(1)y与x之间是否具有线性相关关系?
(2)如果y与x具有线性相关关系,求回归直线方程.
解:(1 )列出下表,并用科学计算器进行计算:
i | 1 | 2 | 3 | 4 | 5 |
xi | 10 | 20 | 30 | 40 | 50 |
yi | 62 | 68 | 75 | 81 | 89 |
xiyi | 620 | 1 360 | 2 250 | 3 240 | 4 450 |
i | 6 | 7 | 8 | 9 | 10 |
xi | 60 | 70 | 80 | 90 | 100 |
yi | 95 | 102 | 108 | 115 | 122 |
xiyi | 5 700 | 7 140 | 8 640 | 10 350 | 12 200 |
![]() =55,
=55,![]() =91.7,
=91.7,![]() xi2=38 500,
xi2=38 500,
![]() yi2=87 777,
yi2=87 777,![]() xiyi=55 950,
xiyi=55 950,
r=
=![]()
≈0.999 8.
从附表3中查出相应于显著水平0.05和n-2的相关系数临界值r0.05=0.632.
由r>r0.05知,y与x具有线性相关关系.
(2)b=
=![]() ≈0.668.
≈0.668.
a=![]() -b
-b![]() =54.96.
=54.96.
即所求回归直线方程为:![]() =0.668x+54.96.
=0.668x+54.96.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
一个车间为了规定工时定额,需要确定加工零件所花费的时间,为此进行了8次试验,收集数据如下:
|
一个车间为了规定工时定额,需要确定加工零件所花费的时间,为此进行了8次试验,收集数据如下:
|
一个车间为了规定工时定额,需要确定加工零件所花费的时间,为此进行了8次试验,收集数据如下:
|
零件个数x(个) |
10 |
20 |
30 |
40 |
50 |
60 |
70 |
80 |
|
加工时间y(分钟) |
62 |
68 |
75 |
81 |
89 |
95 |
102 |
108 |
设回归直线方程为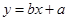 ,则点
,则点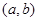 在直线
在直线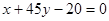 的( )
的( )
A、右上方 B、右下方 C、左上方 D、左下方

