题目内容
一个车间为了规定工时定额,需要确定加工零件所花费的时间,为此进行了5次试验,收集数据如下:
(1)在5次试验中任取2次,记加工时间分别为a、b,求“事件a、b均小于80分钟”的概率;
(2)请根据第二次、第三次、第四次试验的数据,求出y关于x的线性回归方程
=
x+
;
(3)根据(2)得到的线性回归方程预测加工70个零件所需要的时间.
参考公式:
=
,
=
-
其中
=
x1,
=
yt.
| 实验顺序 | 第一次 | 第二次 | 第三次 | 第四次 | 第五次 |
| 零件数x(个) | 10 | 20 | 30 | 40 | 50 |
| 加工时间y(分钟) | 62 | 67 | 75 | 80 | 89 |
(2)请根据第二次、第三次、第四次试验的数据,求出y关于x的线性回归方程
 |
| y |
 |
| b |
 |
| a |
(3)根据(2)得到的线性回归方程预测加工70个零件所需要的时间.
参考公式:
 |
| b |
| |||||||
|
 |
| a |
. |
| y |
 |
| b |
. |
| x |
. |
| x |
| 1 |
| n |
| n |
 |
| t=1 |
. |
| y |
| n |
 |
| t=1 |
分析:(1)确定a,b构成的基本事件、“a,b均小于80分钟”的基本事件的个数,即可求得概率;
(2)分别计算回归系数,利用公式,可得y关于x的线性回归方程
=
x+
;
(3)利用线性回归方程,代入计算可得结论.
(2)分别计算回归系数,利用公式,可得y关于x的线性回归方程
 |
| y |
 |
| b |
 |
| a |
(3)利用线性回归方程,代入计算可得结论.
解答:解:(1)a,b构成的基本事件(a,b)有:(62.67),(62,75),(62,80),(62,89),(67,75),(67,80),(67,89),(75,80),(75,89),(80,89)共有10个. …(2分)
其中“a,b均小于80分钟”的有(62.67),(62,75),(67,75)共3个.…(3分)
∴事件“a,b均小于80分钟”的概率为
.…(4分)
(2)
=
(20+30+40)=30,…(5分)
=
(67+75+80)=74…(6分)
∴
=
=
.…(8分)
∴
=
-
=74-
×30=54.5…(9分)
∴y关于x的线性回归方程y=
x+54.5…(10分)
(3)由(2)知y关于x的线性回归方程为y=
x+54.5,
当x=70时,y=
×70+54.5=100.…(11分)
∴预测加工70个零件需要100分钟的时间.…(12分)
其中“a,b均小于80分钟”的有(62.67),(62,75),(67,75)共3个.…(3分)
∴事件“a,b均小于80分钟”的概率为
| 3 |
| 10 |
(2)
. |
| x |
| 1 |
| 3 |
. |
| y |
| 1 |
| 3 |
∴
 |
| b |
| 20×67+30×75+40×80-3×30×74 |
| 202+302+402-3×302 |
| 13 |
| 20 |
∴
 |
| a |
. |
| y |
 |
| b |
. |
| x |
| 13 |
| 20 |
∴y关于x的线性回归方程y=
| 13 |
| 20 |
(3)由(2)知y关于x的线性回归方程为y=
| 13 |
| 20 |
当x=70时,y=
| 13 |
| 20 |
∴预测加工70个零件需要100分钟的时间.…(12分)
点评:本小题主要考查考查古典概型、线性回归,样本估计总体等知识,以及数据观察能力、抽象思维能力和应用意识.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
一个车间为了规定工时定额,需要确定加工零件所花费的时间,为此进行了8次试验,收集数据如下:
|
一个车间为了规定工时定额,需要确定加工零件所花费的时间,为此进行了8次试验,收集数据如下:
|
一个车间为了规定工时定额,需要确定加工零件所花费的时间,为此进行了8次试验,收集数据如下:
|
零件个数x(个) |
10 |
20 |
30 |
40 |
50 |
60 |
70 |
80 |
|
加工时间y(分钟) |
62 |
68 |
75 |
81 |
89 |
95 |
102 |
108 |
设回归直线方程为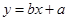 ,则点
,则点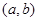 在直线
在直线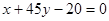 的( )
的( )
A、右上方 B、右下方 C、左上方 D、左下方