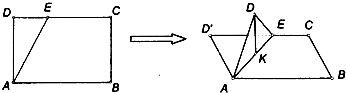
题目内容
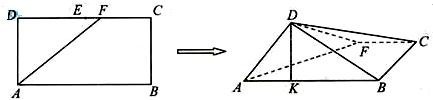
如图,在长方形ABCD中,AB=2,BC=1,E为CD的中点,
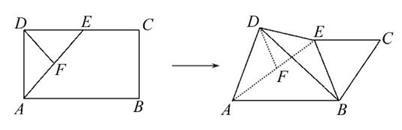
F为AE的中点.现在沿AE将三角形ADE向上折起,在折起的图形中解答下列问题:
(1)在线段AB上是否存在一点K,使BC∥平面DFK?若存在,请证明你的结论;若不存在,请说明理由.
(2)若平面ADE⊥平面ABCE,求证:平面BDE⊥平面ADE.
【解析】(1)线段AB上存在一点K,且当AK=![]() AB时,BC∥平面DFK,
AB时,BC∥平面DFK,
证明如下:
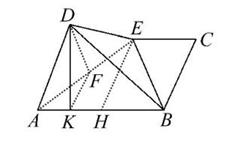
设H为AB的中点,连接EH,则BC∥EH,
又因为AK=![]() AB,F为AE的中点,
AB,F为AE的中点,
所以KF∥EH,所以KF∥BC,
因为KF⊂平面DFK,BC⊄平面DFK,所以BC∥平面DFK.
(2)因为F为AE的中点,DA=DE=1,所以DF⊥AE.
因为平面ADE⊥平面ABCE,所以DF⊥平面ABCE,
因为BE⊂平面ABCE,所以DF⊥BE.
又因为在折起前的图形中E为CD的中点,AB=2,BC=1,所以在折起后的图形中:AE=BE=![]() ,
,
从而AE2+BE2=4=AB2,所以AE⊥BE,
因为AE∩DF=F,所以BE⊥平面ADE,
因为BE⊂平面BDE,所以平面BDE⊥平面ADE.![]()

练习册系列答案
相关题目
 若一个n面体有m个面时直角三角形,则称这个n面体的直度为
若一个n面体有m个面时直角三角形,则称这个n面体的直度为 如图,在长方形ABCD中,AB=
如图,在长方形ABCD中,AB=