题目内容
15.设函数f(x)=ax3+bx-5,其中a,b为常数,若f(-3)=7,则f(3)=-17.分析 由已知可得f(x)+f(-x)=-10,结合f(-3)=7,可得f(3)的值.
解答 解:∵函数f(x)=ax3+bx-5,
∴f(-x)=-ax3-bx-5,
∴f(x)+f(-x)=-10,
∵f(-3)=7,
∴f(3)=-17,
故答案为:-17
点评 本题考查的知识点是奇函数的应用,函数求值,根据已知得到f(x)+f(-x)=-10,是解答的关键.

练习册系列答案
相关题目
3.已知f(x)是定义在R上的奇函数,当x<0时,f(x)=x2+2x,则函数$g(x)=f(x)+\frac{1}{2}x-1$零点的集合为( )
| A. | {1,-1,0} | B. | {-2,2,0} | C. | $\{2,-\frac{1}{2},\frac{{-5+\sqrt{41}}}{4}\}$ | D. | $\{2,\frac{1}{2},\frac{{-5-\sqrt{41}}}{4}\}$ |
20.执行如图所示的程序框图,则输出s的值为( )
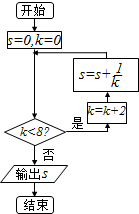

| A. | $\frac{25}{24}$ | B. | $\frac{11}{12}$ | C. | $\frac{5}{6}$ | D. | $\frac{3}{4}$ |