ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩΨίΆ≥ΦΤΘ§ΫΊ÷Ν2016ΡξΒΉ»ΪΙζΈΔ–≈ΉΔ≤α”ΟΜß ΐΝΩ“―Ψ≠ΆΜΤΤ9.27“Ύ.ΈΣΒς≤ι¥σ―ß…ζ’βΗωΈΔ–≈”ΟΜß»ΚΧε÷–ΟΩ»Υ”Β”–ΈΔ–≈»ΚΒΡ ΐΝΩΘ§œ÷¥”Ρ≥ –¥σ―ß…ζ÷–ΥφΜζ≥ι»Γ100ΈΜΆ§―ßΫχ––ΝΥ≥ι―υΒς≤ιΘ§ΫαΙϊ»γœ¬ΘΚ
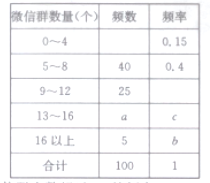
Θ®1Θ©«σ![]() Θ§
Θ§![]() Θ§
Θ§![]() ΒΡ÷ΒΦΑ―υ±Ψ÷–ΈΔ–≈»ΚΗω ΐ≥§Ιΐ12ΒΡΗ≈¬ ΘΜ
ΒΡ÷ΒΦΑ―υ±Ψ÷–ΈΔ–≈»ΚΗω ΐ≥§Ιΐ12ΒΡΗ≈¬ ΘΜ
Θ®2Θ©»τ¥”’β100ΈΜΆ§―ß÷–ΥφΜζ≥ι»Γ2»ΥΘ§«σ’β2»Υ÷–«Γ”–1»ΥΈΔ–≈»ΚΗω ΐ≥§Ιΐ12ΒΡΗ≈¬ ΘΜ
Θ®3Θ©“‘Θ®1Θ©÷–ΒΡΤΒ¬ ΉςΈΣΗ≈¬ Θ§»τ¥”»Ϊ –¥σ―ß…ζ÷–ΥφΜζ≥ι»Γ3»ΥΘ§Φ«![]() ±μ Ψ≥ιΒΫΒΡ «ΈΔ–≈»ΚΗω ΐ≥§Ιΐ12ΒΡ»Υ ΐΘ§«σ
±μ Ψ≥ιΒΫΒΡ «ΈΔ–≈»ΚΗω ΐ≥§Ιΐ12ΒΡ»Υ ΐΘ§«σ![]() ΒΡΖ÷≤ΦΝ–ΦΑ ΐ―ßΤΎΆϊ
ΒΡΖ÷≤ΦΝ–ΦΑ ΐ―ßΤΎΆϊ![]() .
.
ΓΨ¥πΑΗΓΩΘ®1Θ©![]() .Θ®2Θ©
.Θ®2Θ©![]() .Θ®3Θ©ΦϊΫβΈω
.Θ®3Θ©ΦϊΫβΈω
ΓΨΫβΈωΓΩ ‘ΧβΖ÷ΈωΘΚ
(1)άϊ”ΟΤΒ¬ Ζ÷≤Φ±μΩ…ΒΟ![]() Θ§
Θ§![]() Θ§
Θ§![]() .‘ρΈΔ–≈»ΚΗω ΐ≥§Ιΐ12ΒΡΤΒ¬ ΈΣ
.‘ρΈΔ–≈»ΚΗω ΐ≥§Ιΐ12ΒΡΤΒ¬ ΈΣ![]() .
.
(2)”…Χβ“βΩ…ΒΟ2»Υ÷–«Γ”–1»ΥΈΔ–≈»ΚΗω ΐ≥§Ιΐ12ΒΡΗ≈¬ ΈΣ![]() .
.
(3)”…Χβ“βΩ…ΒΟ![]() ΒΡΥυ”–Ω…Ρή»Γ÷Β0Θ§1Θ§2Θ§3.ΫαΚœΗ≈¬ ΙΪ ΫΚΆΕΰœνΖ÷≤ΦΒΡΙΪ ΫΦ¥Ω…«σΒΟΖ÷≤ΦΝ–Θ§»ΜΚσ«σΫβ ΐ―ßΤΎΆϊΩ…ΒΟ
ΒΡΥυ”–Ω…Ρή»Γ÷Β0Θ§1Θ§2Θ§3.ΫαΚœΗ≈¬ ΙΪ ΫΚΆΕΰœνΖ÷≤ΦΒΡΙΪ ΫΦ¥Ω…«σΒΟΖ÷≤ΦΝ–Θ§»ΜΚσ«σΫβ ΐ―ßΤΎΆϊΩ…ΒΟ![]() .
.
‘ΧβΫβΈωΘΚ
Θ®1Θ©‘Ύ0÷Ν4Ηω’β“ΜΕΈΘ§Ε‘”ΠΒΡΤΒ ΐΈΣ15Θ§
”…“―÷ΣΒΟΘΚ![]() Θ§ΫβΒΟ
Θ§ΫβΒΟ![]() Θ§
Θ§
Γύ![]() Θ§
Θ§![]() .ΈΔ–≈»ΚΗω ΐ≥§Ιΐ12ΒΡΤΒ¬ ΈΣ
.ΈΔ–≈»ΚΗω ΐ≥§Ιΐ12ΒΡΤΒ¬ ΈΣ![]() .
.
Θ®2Θ©Φ«ΓΑ2»Υ÷–«Γ”–1»ΥΈΔ–≈»ΚΗω ΐ≥§Ιΐ12Γ±ΈΣ ¬Φΰ![]() Θ§‘ρ
Θ§‘ρ![]() .
.
Υυ“‘Θ§2»Υ÷–«Γ”–1»ΥΈΔ–≈»ΚΗω ΐ≥§Ιΐ12ΒΡΗ≈¬ ΈΣ![]() .
.
Θ®3Θ©“άΧβ“βΩ…÷ΣΘ§ΈΔ–≈»ΚΗω ΐ≥§Ιΐ12ΒΡΗ≈¬ ΈΣ![]() .
.
![]() ΒΡΥυ”–Ω…Ρή»Γ÷Β0Θ§1Θ§2Θ§3.
ΒΡΥυ”–Ω…Ρή»Γ÷Β0Θ§1Θ§2Θ§3.
‘ρ![]() Θ§
Θ§![]() Θ§
Θ§
![]() Θ§
Θ§![]() .
.
ΤδΖ÷≤ΦΝ–»γœ¬ΘΚ
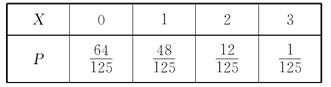
Υυ“‘Θ§![]()
![]() Θ§Μρ
Θ§Μρ![]() .
.

 ‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ
‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ