题目内容
已知双曲线 的左右焦点分别为F1,F2,P为双曲线右支一的任意一点,若
的左右焦点分别为F1,F2,P为双曲线右支一的任意一点,若 的最小值为8a,则双曲线离心率的取值范围是( )
的最小值为8a,则双曲线离心率的取值范围是( )A.(0,+∞)
B.(1,2]
C.

D.(1,3]
【答案】分析:由定义知:|PF1|-|PF2|=2a,|PF1|=2a+|PF2|, =
= =
= ,当且仅当
,当且仅当 ,即|PF2|=2a时取得等号.再利用三线段长的关系,可求得双曲线的离心率的取值范围.
,即|PF2|=2a时取得等号.再利用三线段长的关系,可求得双曲线的离心率的取值范围.
解答:解:∵双曲线 的左右焦点分别为F1,F2,P为双曲线右支一的任意一点
的左右焦点分别为F1,F2,P为双曲线右支一的任意一点
∴|PF1|-|PF2|=2a,|PF1|=2a+|PF2|,
∴ =
= =
= ,
,
当且仅当 ,即|PF2|=2a时取得等号
,即|PF2|=2a时取得等号
∴|PF1|=2a+|PF2|=4a
∵|PF1|-|PF2|=2a<2c,|PF1|+|PF2|=6a≥2c,
∴e∈(1,3]
故选D.
点评:本题考查双曲线的性质和应用,解题时要认真审题,注意基本不等式的合理运用.
 =
= =
= ,当且仅当
,当且仅当 ,即|PF2|=2a时取得等号.再利用三线段长的关系,可求得双曲线的离心率的取值范围.
,即|PF2|=2a时取得等号.再利用三线段长的关系,可求得双曲线的离心率的取值范围.解答:解:∵双曲线
 的左右焦点分别为F1,F2,P为双曲线右支一的任意一点
的左右焦点分别为F1,F2,P为双曲线右支一的任意一点∴|PF1|-|PF2|=2a,|PF1|=2a+|PF2|,
∴
 =
= =
= ,
,当且仅当
 ,即|PF2|=2a时取得等号
,即|PF2|=2a时取得等号∴|PF1|=2a+|PF2|=4a
∵|PF1|-|PF2|=2a<2c,|PF1|+|PF2|=6a≥2c,
∴e∈(1,3]
故选D.
点评:本题考查双曲线的性质和应用,解题时要认真审题,注意基本不等式的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 的左右焦点为
的左右焦点为 ,P为双曲线右支上
,P为双曲线右支上 的最小值为8a,则双曲线的离心率的取值范围是 。
的最小值为8a,则双曲线的离心率的取值范围是 。 的左右焦点分别为
的左右焦点分别为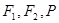 为左支上一点,若
为左支上一点,若 的最小值为
的最小值为 ,则双曲线离心率
,则双曲线离心率 的取值范围为(
)
的取值范围为(
)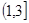 B、
B、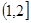 C、
C、 D、
D、
 的左右焦点分别是
的左右焦点分别是 ,
, 点是双曲线右支上一点,且
点是双曲线右支上一点,且 ,则三角形
,则三角形 的面积等于
的面积等于