题目内容
【题目】已知曲线C的极坐标方程是ρ=2cosθ,以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线l的参数方程是 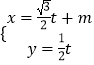 (t为参数).
(t为参数).
(1)求曲线C的直角坐标方程和直线l的普通方程;
(2)设点P(m,0),若直线l与曲线C交于A,B两点,且|PA||PB|=1,求实数m的值.
【答案】
(1)解:由ρ=2cosθ,得:ρ2=2ρcosθ,∴x2+y2=2x,即(x﹣1)2+y2=1,
∴曲线C的直角坐标方程为(x﹣1)2+y2=1.
由  (t为参数),得x=
(t为参数),得x= ![]() ,即x﹣
,即x﹣ ![]() ,
,
∴直线l的普通方程为x﹣ ![]() .
.
(2)解:将  代入(x﹣1)2+y2=1,得:(
代入(x﹣1)2+y2=1,得:( ![]() )2+(
)2+( ![]() )2=1,
)2=1,
整理得: ![]() ,由△>0,即3(m﹣1)2﹣4(m2﹣2m)>0,
,由△>0,即3(m﹣1)2﹣4(m2﹣2m)>0,
解得:﹣1<m<3.设t1,t2是上述方程的两实根,则 ![]() ,t1t2=m2﹣2m,
,t1t2=m2﹣2m,
又直线l过点P(m,0),由上式及t的几何意义得|PA||PB|=|t1t2|=|m2﹣2m|=1,
解得:m=1或m=1 ![]() ,都符合﹣1<m<3,
,都符合﹣1<m<3,
因此实数m的值为1或1+ ![]() 或1﹣
或1﹣ ![]() .
.
【解析】(1)由ρ=2cosθ,得:ρ2=2ρcosθ,由此能求出曲线C的直角坐标方程,直线l的参数方程中消去参数得到其普通方程.(2)首先把圆的极坐标方程化为直角坐标方程,把直线的参数方程中的参数t消去化为普通方程,把直线的参数方程代入圆的标准方程得到关于t的一元二次方程,由于直线与圆有两个交点,方程有两个实根,所以要求判别式为正,解得m的范围,利用根与系数关系表示t1t2,利用直线的参数方程参数t的几何意义可知|PA||PB|=|t1t2|=|m2﹣2m|=1,解出m后要求符合m的范围即可;

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目