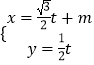题目内容
【题目】已知函数f（x）=2sin（ωx+φ）+1（ω＞0，|φ|≤ 
），其图象与直线y=﹣1相邻两个交点的距离为π，若f（x）＞1对x∈（﹣ 
， 
）恒成立，则φ的取值范围是（ ）
A.
B.
C.
D.
【答案】D
【解析】解：函数f（x）=2sin（ωx+φ）+1（ω＞0，|φ|≤ 
），其图象与直线y=﹣1相邻两个交点的距离为π，
故函数的周期为 
=π，∴ω=2，f（x）=2sin（2x+φ）+1．
若f（x）＞1对x∈（﹣ 
， 
）恒成立，即当x∈（﹣ ， ）时，sin（2x+φ）＞0恒成立，
故有2kπ＜2（﹣ ）+φ＜2 +φ＜2kπ+π，求得2kπ+ 
φ＜2kπ+ ，k∈Z，
结合所给的选项，
故选：D．
练习册系列答案
相关题目
