题目内容
已知关于x的函数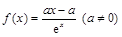
(1)当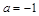 时,求函数
时,求函数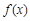 的极值;
的极值;
(2)若函数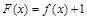 没有零点,求实数a取值范围.
没有零点,求实数a取值范围.
(1)函数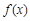 的极小值为
的极小值为 ;(2)
;(2)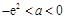 .
.
解析试题分析:(1)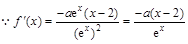 ,当
,当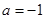 时,
时,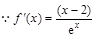
可利用导函数的符号判断函数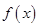 的单调性并求得极值;
的单调性并求得极值;
(2)要使函数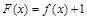 没有零点,可借助导数研究函数
没有零点,可借助导数研究函数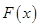 的单调性及极值,参数
的单调性及极值,参数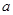 的值要确保
的值要确保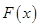 在定义域内恒正(或恒负),即函数
在定义域内恒正(或恒负),即函数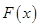 的最小值为正,或最大值为负,并由此求出
的最小值为正,或最大值为负,并由此求出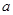 的取值范围.
的取值范围.
试题解析:
解:(1)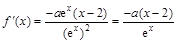 ,
,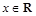 . 2分
. 2分
当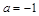 时,
时,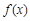 ,
,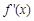 的情况如下表:
的情况如下表:
所以,当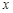
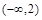
2 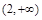
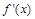
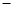
0 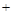
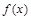
↘ 极小值 ↗ 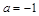 时,函数
时,函数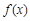 的极小值为
的极小值为 . 6分
. 6分
(2)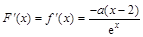 . 7分
. 7分
当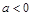 时,
时,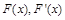 的情况如下表:
的情况如下表: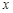
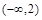
2 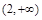
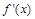
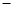
 练习册系列答案
练习册系列答案
快乐假期高考状元假期学习方案寒假系列答案
创新学习寒假作业东北师范大学出版社系列答案
寒假零距离系列答案
高效中考安徽师范大学出版社系列答案
新编高中假期作业四川师范大学电子出版社系列答案
授之以渔中考复习方案系列答案
中考提分攻略系列答案
寒假天地寒假作业本延边大学出版社系列答案
寒假作业广东人民出版社系列答案
快乐寒假东南大学出版社系列答案
相关题目
 为函数
为函数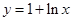 图象上一点,O为坐标原点,记直线
图象上一点,O为坐标原点,记直线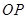 的斜率
的斜率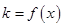 .
.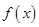 在区间
在区间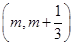
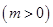 上存在极值,求实数m的取值范围;
上存在极值,求实数m的取值范围;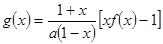 ,若对任意
,若对任意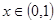 恒有
恒有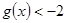 ,求实数
,求实数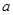 的取值范围.
的取值范围. -(2+a)lnx(a≥0).
-(2+a)lnx(a≥0). 与直线
与直线 ,
, ,
, 所围成平面图形的面积.
所围成平面图形的面积.
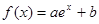 在
在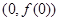 处切线为
处切线为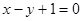 .
.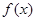 的解析式;
的解析式;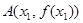 ,
,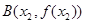 ,
,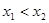 ,
,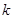 表示直线
表示直线 的斜率,求证:
的斜率,求证: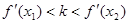 .
. ,函数
,函数 是区间
是区间 上的减函数.
上的减函数. 的最大值;
的最大值; 恒成立,求
恒成立,求 的取值范围;
的取值范围;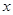 的方程
的方程 的根的个数.
的根的个数.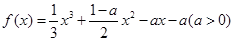 .
.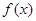 在区间(-2,0)内恰有两个零点,求a的取值范围;
在区间(-2,0)内恰有两个零点,求a的取值范围;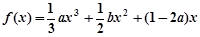 ,
,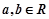 ,
,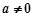 ,
, 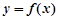 与
与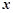 轴相切于异于原点的一点,且函数
轴相切于异于原点的一点,且函数 的极小值为
的极小值为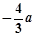 ,求
,求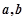 的值;
的值;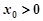 ,且
,且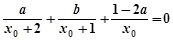 ,
,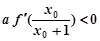 ; ②求证:
; ②求证: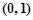 上存在极值点.
上存在极值点.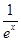 -
-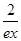 成立.
成立.