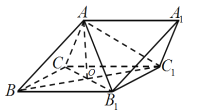
题目内容
【题目】如图,已知直线![]() 关于直线
关于直线![]() 对称的直线为
对称的直线为![]() ,直线
,直线![]() 与椭圆
与椭圆![]() 分别交于点
分别交于点![]() 、
、![]() 和
和![]() 、
、![]() ,记直线
,记直线![]() 的斜率为
的斜率为![]() .
.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)当![]() 变化时,试问直线
变化时,试问直线![]() 是否恒过定点? 若恒过定点,求出该定点坐标;若不恒过定点,请说明理由.
是否恒过定点? 若恒过定点,求出该定点坐标;若不恒过定点,请说明理由.

【答案】(Ⅰ)1;(Ⅱ)![]() .
.
【解析】试题分析:(Ⅰ)可以设直线![]() 的方程为
的方程为![]() ,再设直线
,再设直线![]() 上任意一点
上任意一点![]() 关于直线
关于直线![]() 对称点为
对称点为![]() ,于是分别表示出
,于是分别表示出![]() ,由直线对称性可知,
,由直线对称性可知, ![]() 所在直线与
所在直线与![]() 垂直,且
垂直,且![]() 中点在
中点在![]() 上,于是整理得出
上,于是整理得出![]() 的值;(Ⅱ)本问考查椭圆中直线过定点问题,设
的值;(Ⅱ)本问考查椭圆中直线过定点问题,设![]() ,将AM方程与椭圆方程联立,可以求出点M的坐标,同理将直线AN方程与椭圆方程联立,可以求出点N的坐标,根据M,N两点坐标,可以求出直线MN的方程,从而判定直线MN是否过定点.
,将AM方程与椭圆方程联立,可以求出点M的坐标,同理将直线AN方程与椭圆方程联立,可以求出点N的坐标,根据M,N两点坐标,可以求出直线MN的方程,从而判定直线MN是否过定点.
试题解析:(Ⅰ)设直线![]() 上任意一点
上任意一点![]() 关于直线
关于直线![]() 对称点为
对称点为![]()

直线![]() 与直线
与直线![]() 的交点为
的交点为![]() ,∴
,∴![]()
![]() ,由
,由![]()
得![]() ……..①
……..①
由![]() 得
得![]() …….②,
…….②,
由①②得 ![]()
![]() .
.
(Ⅱ)设点![]() ,由
,由 得
得![]() ,
,
∴![]() ,∴
,∴![]() .
.
同理: ![]() ,
, ![]()

![]() ,∴
,∴![]()
即: 
∴当![]() 变化时,直线
变化时,直线![]() 过定点
过定点![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某班主任为了对本班学生的月考成绩进行分析,从全班40名同学中随机抽取一个容量为6的样本进行分析.随机抽取6位同学的数学、物理分数对应如表:
学生编号 | 1 | 2 | 3 | 4 | 5 | 6 |
数学分数x | 60 | 70 | 80 | 85 | 90 | 95 |
物理分数y | 72 | 80 | 88 | 90 | 85 | 95 |
(1)根据上表数据用散点图说明物理成绩y与数学成绩x之间是否具有线性相关性?
(2)如果具有线性相关性,求出线性回归方程(系数精确到0.1);如果不具有线性相关性,请说明理由.
(3)如果班里的某位同学数学成绩为50,请预测这位同学的物理成绩。
![]() (附
(附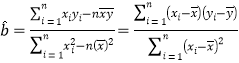 )
)
【题目】某种产品的质量以其“无故障使用时间![]() (单位:小时)”衡量,无故障使用时间越大表明产品质量越好,且无故障使用时间大于3小时的产品为优质品,从某企业生产的这种产品中抽取100件,并记录了每件产品的无故障使用时间,得到下面试验结果:
(单位:小时)”衡量,无故障使用时间越大表明产品质量越好,且无故障使用时间大于3小时的产品为优质品,从某企业生产的这种产品中抽取100件,并记录了每件产品的无故障使用时间,得到下面试验结果:
无故障使用时间 |
|
|
|
频数 | 20 | 40 | 40 |
以试验结果中无故障使用时间落入各组的频率作为一件产品的无故障使用时间落入相应组的概率.
(1)从该企业任取两件这种产品,求至少有一件是优质品的概率;
(2)若该企业生产的这种产品每件销售利润![]() (单位:元)与其无故障使用时间
(单位:元)与其无故障使用时间![]() 的关系式为
的关系式为
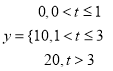
从该企业任取两件这种产品,其利润记为![]() (单位:元),求
(单位:元),求![]() 的分布列与数学期望.
的分布列与数学期望.