题目内容
【题目】已知等差数列![]() 与等比数列
与等比数列![]() 是非常数的实数列,设
是非常数的实数列,设![]() .
.
(1)请举出一对数列![]() 与
与![]() ,使集合
,使集合![]() 中有三个元素;
中有三个元素;
(2)问集合![]() 中最多有多少个元素?并证明你的结论;
中最多有多少个元素?并证明你的结论;
【答案】(1) ![]() .
.
(2)3个,证明见解析.
【解析】分析:(1)![]() ,则
,则![]() ;(2)不妨设
;(2)不妨设![]() ,由
,由![]() ,令
,令![]() ,原问题转化为
,原问题转化为![]() 关于的方程
关于的方程![]() 最多有多少个解,可以证明当
最多有多少个解,可以证明当![]() 时,方程①最多有
时,方程①最多有![]() 个解:
个解:![]() 时,方程①最多有
时,方程①最多有![]() 个解,从而可得结果.
个解,从而可得结果.
详解:(1)![]() ,则
,则![]()
(2)不妨设![]() ,由
,由![]()
令![]() ,原问题转化为
,原问题转化为![]() 关于的方程
关于的方程
![]() ①
①
最多有多少个解.
下面我们证明:当![]() 时,方程①最多有
时,方程①最多有![]() 个解:
个解:![]() 时,方程①最多有
时,方程①最多有![]() 个解
个解
当![]() 时,考虑函数
时,考虑函数![]() ,则
,则![]()
如果![]() ,则
,则![]() 为单调函数,故方程①最多只有一个解;
为单调函数,故方程①最多只有一个解;
如果![]() ,且不妨设由
,且不妨设由![]() 得
得![]() 由唯一零点
由唯一零点![]() ,于是当
,于是当![]() 时,
时,
![]() 恒大于
恒大于![]() 或恒小于
或恒小于![]() ,当
,当![]() 时,
时,![]() 恒小于
恒小于![]() 或恒大于
或恒大于![]()
这样![]() 在区间
在区间![]() 与
与![]() 上是单调函数,故方程①最多有
上是单调函数,故方程①最多有![]() 个解
个解
当![]() 时,如果
时,如果![]()
如果![]() 为奇数,则方程①变为
为奇数,则方程①变为
![]()
显然方程最多只有一个解,即最多只有一个奇数满足方程①
如果![]() 为偶数,则方程①变为
为偶数,则方程①变为
![]() ,由
,由![]() 的情形,上式最多有
的情形,上式最多有![]() 个解,即满足①的偶数最多有
个解,即满足①的偶数最多有![]() 个
个
这样,最多有![]() 个正数满足方程①
个正数满足方程①
对于![]() ,同理可以证明,方程①最多有
,同理可以证明,方程①最多有![]() 个解.
个解.
综上所述,集合![]() 中的元素个数最多有
中的元素个数最多有![]() 个.
个.
再由(1)可知集合![]() 中的元素个数最多有
中的元素个数最多有![]() 个.
个.

【题目】汽车的普及给人们的出行带来了诸多方便,但汽车超速行驶也造成了诸多隐患.为了解某一段公路汽车通过时的车速情况,现随机抽测了通过这段公路的200辆汽车的时速,所得数据均在区间![]() 中,其频率分布直方图如图所示.
中,其频率分布直方图如图所示.
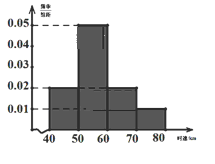
(1)求被抽测的200辆汽车的平均时速.
(2)该路段路况良好,但属于事故高发路段,交警部门对此路段过往车辆限速![]() .对于超速行驶,交警部门对超速车辆有相应处罚:记分(扣除驾驶员驾照的分数)和罚款.罚款情况如下:
.对于超速行驶,交警部门对超速车辆有相应处罚:记分(扣除驾驶员驾照的分数)和罚款.罚款情况如下:
超速情况 | 10%以内 | 10%~20% | 20%~50% | 50%以上 |
罚款情况 | 0元 | 100元 | 150元 | 可以并处吊销驾照 |
①求被抽测的200辆汽车中超速在10%~20%的车辆数.
②该路段车流量比较大,按以前统计该路段每天来往车辆约2000辆.试预估每天的罚款总数.