题目内容
已知椭圆的中心在原点，焦点在x轴上，且长轴长为12，离心率为
，则椭圆的方程是
- A.
+
=1 - B.
+
=1 - C.
+
=1 - D.+
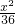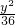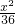=1
D
分析：依题意可知c，进而根据离心率求得a，进而根据b2=a2-c2求得b20，则椭圆方程可得．
解答：由题意知，2a=12，a=6，
∴e=
=
=，
∴c=2，
从而b2=a2-c2=32，
∴方程是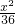+=1．
故选D．
点评：本题主要考查了椭圆的标准方程．解题的关键是熟练掌握椭圆标准方程中a，b和c之间的关系．
分析：依题意可知c，进而根据离心率求得a，进而根据b2=a2-c2求得b20，则椭圆方程可得．
解答：由题意知，2a=12，a=6，
∴e=
==，∴c=2，
从而b2=a2-c2=32，
∴方程是
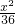+=1．故选D．
点评：本题主要考查了椭圆的标准方程．解题的关键是熟练掌握椭圆标准方程中a，b和c之间的关系．
练习册系列答案
相关题目