题目内容
已知向量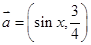 ,
,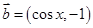 .
.
(1)当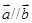 时,求
时,求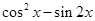 的值;
的值;
(2)设函数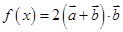 ,已知在
,已知在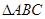 中,内角
中,内角 、
、 、
、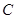 的对边分别为
的对边分别为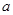 、
、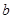 、
、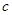 ,若
,若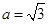 ,
,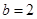 ,
,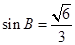 ,求
,求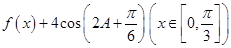 的取值范围.
的取值范围.
(1)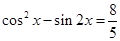 ;(2)
;(2)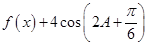 在
在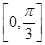 上的取值范围是
上的取值范围是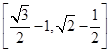 .
.
解析试题分析:(1)利用向量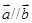 求出
求出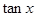 的值,然后利用弦化切的思想计算
的值,然后利用弦化切的思想计算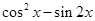 的值;(2)先将函数
的值;(2)先将函数 的解析式求出并化简为
的解析式求出并化简为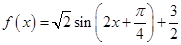 ,然后利用正弦定理结合边角关系求出
,然后利用正弦定理结合边角关系求出 的值,从而确定函数
的值,从而确定函数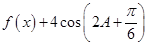 的解析式,然后由
的解析式,然后由 计算出
计算出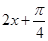 的取值范围,最终利用正弦曲线即可确定函数
的取值范围,最终利用正弦曲线即可确定函数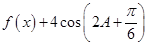 在
在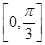 上的取值范围.
上的取值范围.
试题解析:(1)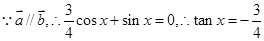 2分
2分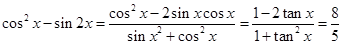 6分
6分
(2)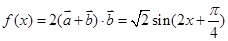 +
+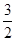
由正弦定理得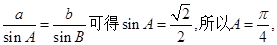 或
或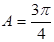 9分
9分
因为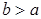 ,所以
,所以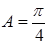 10分
10分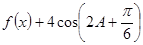
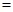
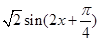
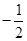 ,
,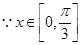
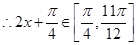 ,
,
所以 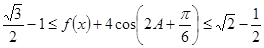 13分
13分
考点:1.平面向量共线的坐标表示;2.弦化切;3.三角函数的值域;4.正弦定理

练习册系列答案
相关题目
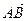 |=2|
|=2|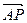 |,则点P的坐标为____________.
|,则点P的坐标为____________. 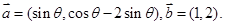
 ,求
,求 的值;
的值;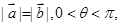 求
求 的值。
的值。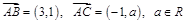
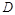 为
为 的中点,
的中点,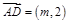 ,求
,求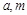 的值;
的值; 是以
是以 为斜边的直角三角形,求
为斜边的直角三角形,求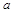 的值.
的值. .
. ,求
,求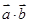 的值;
的值;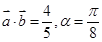 ,且
,且 ,求
,求 的值.
的值.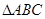 的三个内角
的三个内角 所对的边分别为a,b,c,向量
所对的边分别为a,b,c,向量 ,
, ,且
,且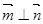 .
. 的大小;
的大小; ,
,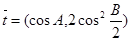 ,试求
,试求 的取值范围
的取值范围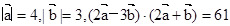 ,
,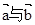 的夹角
的夹角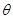 ; (2)求
; (2)求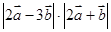 的值.
的值.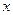 ),b=(2
),b=(2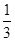 AC,在AB上取一点M,使得AM=
AC,在AB上取一点M,使得AM=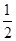 BN,在CM的延长线上取点Q,使得
BN,在CM的延长线上取点Q,使得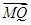 =λ
=λ 时,
时, =
= ,试确定λ的值.
,试确定λ的值.