题目内容
2.复数$\frac{5}{2-i}$的共轭复数是( )| A. | 1-2i | B. | 1+2i | C. | 2+i | D. | 2-i |
分析 利用复数的运算法则、共轭复数的定义即可得出.
解答 解:∵复数$\frac{5}{2-i}$=$\frac{5(2+i)}{(2-i)(2+i)}$=$\frac{5(2+i)}{5}$=2+i,
∴其共轭复数为2-i.
故选:D.
点评 本题考查了复数的运算法则、共轭复数的定义,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
10.函数y=lg(x2-x)的定义域为( )
| A. | {x|x≤0,或x≥1} | B. | {x|x<0,或x>1} | C. | {x|0≤x≤1} | D. | {x|0<x<1} |
17.某种产品的广告费支出x(单位:百万元)与销售额y(单位:百万元)之间有如下对应数据:
(1)求y关于x的回归直线方程.
(2)并预测广告费支出700万元的销售额大约是多少万元?
(参考公式:$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n•\overline{x}•\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n•\overline{{x}^{2}}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$•$\overline{x}$)
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 60 | 50 | 70 |
(2)并预测广告费支出700万元的销售额大约是多少万元?
(参考公式:$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n•\overline{x}•\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n•\overline{{x}^{2}}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$•$\overline{x}$)
11.记sin35°=a,则tan2015°的值等于( )
| A. | $\frac{a}{{\sqrt{1-{a^2}}}}$ | B. | $\frac{-a}{{\sqrt{1-{a^2}}}}$ | C. | $\frac{{\sqrt{1-{a^2}}}}{a}$ | D. | $\frac{{-\sqrt{1-{a^2}}}}{a}$ |
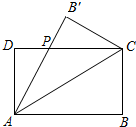 春兰公司为一家制冷设备厂设计生产一种长方形薄板,其周长为4米,这种薄板须沿其对角线折叠后使用.如图所示,ABCD(AB>AD)为长方形薄板,沿AC折叠后,AB′交DC于点P.当△ADP的面积最大时最节能.
春兰公司为一家制冷设备厂设计生产一种长方形薄板,其周长为4米,这种薄板须沿其对角线折叠后使用.如图所示,ABCD(AB>AD)为长方形薄板,沿AC折叠后,AB′交DC于点P.当△ADP的面积最大时最节能.