题目内容
13.一家冷饮厂每个月都要对大型冰激凌机进行维修,维修人员发现,维修费用与时间的关系:第n个月的维修费2(n-1)+500元,这种冰激凌机的售价为50万元,使用5年后报废,那么这台冰激凌机从投入使用到报废,每天的消耗是多少(一年按360天计算,结果保留3位有效数字)?分析 由题意利用等差数列的求和公式求出5年共60个月的维修费,加上购买机器的总费用求出机器从投入生产到报废共付出的维修费用与购买费用之和,除以总天数后得到答案.
解答 解:这种冰激凌机从投入生产到报废共付出的维修费用:500+(2+500)+(4+500)+…+(118+500)
=500×60+(2+4+…+118)=30000+$\frac{(2+118)×59}{2}$=30000+60×59=33540元.
买这种冰激凌机花费500000元.
所以机器从投入生产到报废共付出的维修费用与购买费用之和为500000+33540=533540元.
5年共计5×360=1800天.
所以,每天的消耗是$\frac{533540}{1800}$≈296元.
点评 本题考查了函数模型的选择及应用,考查了等差数列的求和,考查了运算能力和对实际问题的理解能力,是中档题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
3.全集U={0,1,2,3,4},集合A={1,2,3},则∁UA为( )
| A. | {0,4} | B. | {1,2,3} | C. | {0,1,2,3,4} | D. | {2} |
4.下列条件中,能判断两个平面平行的是( )
| A. | 一个平面内有无数条直线平行于另一个平面 | |
| B. | 一个平面内有两条直线平行于另一个平面 | |
| C. | 一个平面内有两条相交直线平行于另一个平面 | |
| D. | 两个平面同时垂直于另一个平面 |
1.如图所示,在正面体ABCD-A1B1C1D1中,AD1∩A1D=O,则线段CO在平面AD1内的射影是( )
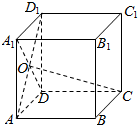

| A. | 线段DO | B. | 线段D1O | C. | 线段A1O | D. | 线段AO |
8.若复数z满足z(6-8i)=|8+6i|(i是虚数单位),则z的虚部为( )
| A. | $\frac{4}{5}$ | B. | 4 | C. | -$\frac{4}{5}$ | D. | -4 |
18.若AB∥A′B′,AC∥A′C′,则有( )
| A. | ∠BAC=∠B′A′C′ | |
| B. | ∠BAC+∠B′A′C′=180° | |
| C. | ∠BAC=∠B′A′C′或∠BAC+∠B′A′C′=180° | |
| D. | ∠BAC>∠B′A′C′ |