题目内容
如图①,四边形ABCD为等腰梯形,AE⊥DC,AB=AE=
DC,F为EC的中点,现将△DAE沿AE翻折到△PAE的位置,如图②,且平面PAE⊥平面ABCE.
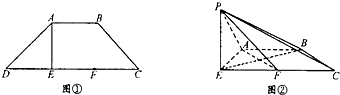
(Ⅰ)求证:平面PAF⊥平面PBE;
(Ⅱ)求三棱锥A-PBC与E-BPF的体积之比.
| 1 | 3 |

(Ⅰ)求证:平面PAF⊥平面PBE;
(Ⅱ)求三棱锥A-PBC与E-BPF的体积之比.
分析:(I)先证明四边形AEFB为正方形,可证得BE⊥AF;再利用面面垂直的性质,证得线面垂直,再得PE⊥AF,由此可证AF⊥平面PBE,从而证明面面垂直;
(II)根据VA-PBC=VP-ABC,VE-BPF=VP-BEF,只需判断三棱锥P-ABC与P-BEF的高和底面△ABC与△BEF的面积的数量关系,可得三棱锥A-PBC与E-BPF的体积之比.
(II)根据VA-PBC=VP-ABC,VE-BPF=VP-BEF,只需判断三棱锥P-ABC与P-BEF的高和底面△ABC与△BEF的面积的数量关系,可得三棱锥A-PBC与E-BPF的体积之比.
解答: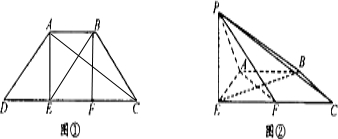 解:(I)证明:∵EF∥AB,AB=EF=
解:(I)证明:∵EF∥AB,AB=EF=
CD,
∴四边形AEFB为平行四边形,又AE=AB,AE⊥CD,
∴四边形AEFB为正方形,∴BE⊥AF,
∴平面PAE⊥平面ABCE,PE⊥AE,平面PAE∩平面ABCE=AE,
∴PE⊥平面ABCE,∴PE⊥AF,
又PE∩BE=E,∴AF⊥平面PBE,AF?平面PAF,
∴平面PBE⊥平面PAF.
(II)∵VA-PBC=VP-ABC,
VE-BPF=VP-BEF,
∵三棱锥P-ABC与P-BEF的高相等,
底面△ABC与△BEF的面积也相等,
∴三棱锥A-PBC与E-BPF的体积之比为1:1.
 解:(I)证明:∵EF∥AB,AB=EF=
解:(I)证明:∵EF∥AB,AB=EF=| 1 |
| 3 |
∴四边形AEFB为平行四边形,又AE=AB,AE⊥CD,
∴四边形AEFB为正方形,∴BE⊥AF,
∴平面PAE⊥平面ABCE,PE⊥AE,平面PAE∩平面ABCE=AE,
∴PE⊥平面ABCE,∴PE⊥AF,
又PE∩BE=E,∴AF⊥平面PBE,AF?平面PAF,
∴平面PBE⊥平面PAF.
(II)∵VA-PBC=VP-ABC,
VE-BPF=VP-BEF,
∵三棱锥P-ABC与P-BEF的高相等,
底面△ABC与△BEF的面积也相等,
∴三棱锥A-PBC与E-BPF的体积之比为1:1.
点评:本题考查了面面垂直的证明,考查了棱锥的体积公式,利用三棱锥的换底性求三棱锥的体积是常用方法.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
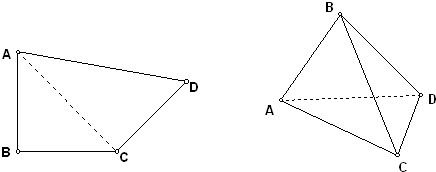 如图,平面四边形ABCD中,AB=BC=CD=a,∠B=90°,∠C=135°,沿对角线AC将△ABC折起,使平面ABC与平面ACD互相垂直.
如图,平面四边形ABCD中,AB=BC=CD=a,∠B=90°,∠C=135°,沿对角线AC将△ABC折起,使平面ABC与平面ACD互相垂直. (1)如图,平行四边形ABCD中,M、N分别为DC、BC的中点,已知
(1)如图,平行四边形ABCD中,M、N分别为DC、BC的中点,已知 如图,已知△ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行四边形,DC⊥平面ABC,AB=2,
如图,已知△ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行四边形,DC⊥平面ABC,AB=2, 在平面直角坐标系xoy中,已知四边形OABC是平行四边形,A(4,0),C(1,
在平面直角坐标系xoy中,已知四边形OABC是平行四边形,A(4,0),C(1,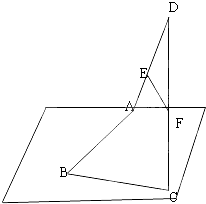 已知:如图,空间四边形ABCD中,E、F分别是DA、DC的中点.求证:EF∥平面ABC.
已知:如图,空间四边形ABCD中,E、F分别是DA、DC的中点.求证:EF∥平面ABC.