题目内容
设函数 (
( )的图象关于原点对称,且
)的图象关于原点对称,且 时,
时, 取极小值
取极小值 ,
,
①求 的值;
的值;
②当 时,图象上是否存在两点,使得过此两点处的切线互相垂直?试证明你的结论。
时,图象上是否存在两点,使得过此两点处的切线互相垂直?试证明你的结论。
③若 ,求证:
,求证: 。
。
① 函数
函数 的图象关于原点对称
的图象关于原点对称
 对任意实数
对任意实数 ,有
,有


即 恒成立
恒成立 


 时,
时, 取极小值
取极小值 ,
, 且
且

②当 时,图象上不存在这样的两点使结论成立。
时,图象上不存在这样的两点使结论成立。
假设图象上存在两点 ,使得过此两点处的切线互相垂直,则由
,使得过此两点处的切线互相垂直,则由 知两点处的切线斜率分别为
知两点处的切线斜率分别为
且 (*)
(*)
 [-1,1]
[-1,1] 与(*)矛盾
与(*)矛盾
③ 令
令 得
得 ,
,
或 时,
时, ,
,  时
时

 在[-1,1]上是减函数,且
在[-1,1]上是减函数,且 ……10分
……10分

 在[-1,1]上
在[-1,1]上
 时,
时,

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 ,AC=
,AC= ,BC⊥AD, 则三棱锥的外接球的体积为 =_____________.
,BC⊥AD, 则三棱锥的外接球的体积为 =_____________. 的值等于( )
的值等于( ) B.
B. C.
C. D.
D.
 .
. ,且
,且 ,求
,求 的值;
的值; 的最小正周期及单调递增区间.
的最小正周期及单调递增区间. ,则角α值为( )
,则角α值为( )

 B.
B. C.
C. D.
D.
 , 则△ABC的形状为 ( )
, 则△ABC的形状为 ( )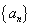 的前n项和为
的前n项和为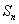 ,满足
,满足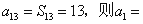 ( )
( )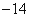 B.
B.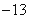 C.
C.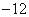 D.
D.