题目内容
已知命题p:lg(x2-2x-2)≥0;命题q:
<-1,若命题p是真命题,命题q是假命题,则实数x的取值范围是
| 4 | x-4 |
x≥4或x≤-1
x≥4或x≤-1
.分析:分别按照要求求出命题p是真命题,命题q是假命题时对应的x的取值范围,然后求交集.
解答:解:由lg(x2-2x-2)≥0得x2-2x-2≥1,即x2-2x-3≥0,解得x≥3或x≤-1,即p:x≥3或x≤-1.
由
<-1,得
<0,解得0<x<4,即q:0<x<4.
因为q是假命题,所以¬q:x≤0或x≥4.
又p是真命题,所以x≥3或x≤-1.
解得x≥4或x≤-1.
故答案为:x≥4或x≤-1.
由
| 4 |
| x-4 |
| x |
| x-4 |
因为q是假命题,所以¬q:x≤0或x≥4.
又p是真命题,所以x≥3或x≤-1.
解得x≥4或x≤-1.
故答案为:x≥4或x≤-1.
点评:本题主要考查命题真假的判断和应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知命题P:lg(x-1)<0,命题Q:|1-2x|<2,则P是Q的( )
| A、充分不必要条件 | B、必要不充分条件 | C、充要条件 | D、既不充分也不必要条件 |
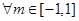 ,不等式a2-5a-3≥
,不等式a2-5a-3≥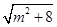 恒成立,若命题“P或Q”为真命题,且“P且Q”为假命题,求实数a的范围。
恒成立,若命题“P或Q”为真命题,且“P且Q”为假命题,求实数a的范围。