Question

【题目】已知椭圆的离心率为，且以原点为圆心，以短轴长为直径的圆过点.

（1）求椭圆的标准方程；

（2）若过点的直线与椭圆交于不同的两点，且与圆没有公共点，设为椭圆上一点，满足（为坐标原点），求实数的取值范围.

Answer 1

【答案】（1）（2）

【解析】

（1）利用直线与圆相切的充要条件列出方程求出的值，利用椭圆的离心率公式得到，的关系，再利用椭圆本身三个参数的关系求出，的值，将，的值代入椭圆的方程即可；

（2）设的方程代入椭圆方程，利用确定，，三点之间的关系，利用点在椭圆上，建立方程，从而可求实数取值范围．

（1）以原点为圆心，椭圆的短半轴长为半径的圆与直线相切

根据点到直线距离公式可得：

椭圆的离心率为

椭圆C的方程为：

（2）由题意直线斜率不为，

设直线：

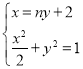得

由得

，

设，

由韦达定理

点在椭圆上

得①

直线与圆没有公共点，则，

.②

由①②可得：