题目内容
已知二次函数 ,且不等式
,且不等式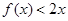 的解集为
的解集为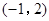 .(1) 方程
.(1) 方程 有两个相等的实根,求
有两个相等的实根,求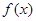 的解析式.(2)
的解析式.(2) 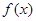 的最小值不大于
的最小值不大于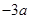 ,求实数
,求实数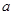 的取值范围.(3)
的取值范围.(3) 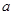 如何取值时,函数
如何取值时,函数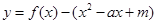 (
(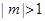 )存在零点,并求出零点.
)存在零点,并求出零点.
(1) 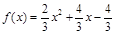 ;(2)
;(2)
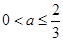 ;(3)当
;(3)当 时有一个零点;当
时有一个零点;当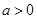 且
且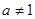 时有2个零点.
时有2个零点.
【解析】
试题分析:(1)因为 的解集为
的解集为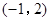 ,所以-1和2是方程f(x)-2x=0的两个根,得到a、b、c之间的关系,又由于方程
,所以-1和2是方程f(x)-2x=0的两个根,得到a、b、c之间的关系,又由于方程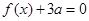 有两个相等的实根,所以利用判别式为0可以求出a、b、c的值,从而求出函数解析式.(2)因为函数图像是开口向上的抛物线,所以最小值在顶点处取得,所以得到顶点的纵坐标后,让纵坐标小于等于-3a就行了.(3)先判断方程是不是一元二次方程,如果是一元一次方程就直接求方程的根,如果是一元二次方程就需要讨论判别式,讨论方程是不是有根.
有两个相等的实根,所以利用判别式为0可以求出a、b、c的值,从而求出函数解析式.(2)因为函数图像是开口向上的抛物线,所以最小值在顶点处取得,所以得到顶点的纵坐标后,让纵坐标小于等于-3a就行了.(3)先判断方程是不是一元二次方程,如果是一元一次方程就直接求方程的根,如果是一元二次方程就需要讨论判别式,讨论方程是不是有根.
试题解析:∵ 的解集为
的解集为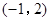 ,
,
∴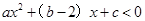 的解集为
的解集为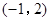 ,
1分
,
1分
∴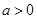 ,且方程
,且方程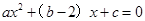 的两根为
的两根为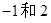
即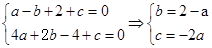 ,∴
,∴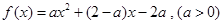 2分
2分
(1)∵方程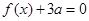 有两个相等的实根,即
有两个相等的实根,即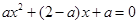 有两个相等的实根
有两个相等的实根
∴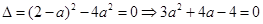 ,
,
∴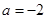 或
或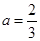 3分
3分
∵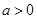 ,∴
,∴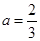 , ∴
, ∴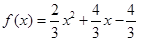 4分
4分
(2)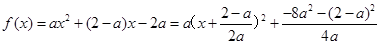
∵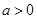 ,∴
,∴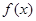 的最小值为
的最小值为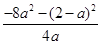 ,
5分
,
5分
则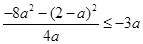 ,
, ,解得
,解得 , 7分
, 7分
∵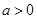 ,∴
,∴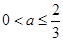 8分
8分
(3)由 ,得
,得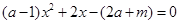 (※)
(※)
①当 时,方程(※) 有一解
时,方程(※) 有一解 ,
,
函数 有一零点
有一零点 ;
9分
;
9分
②当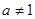 时,
时, 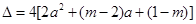
方程(※)有一解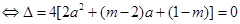 , 令
, 令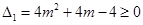
得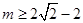 或
或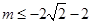 , ∵
, ∵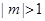 即
即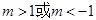 ,
,
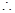 i)当
i)当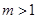 ,
,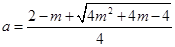 时,
时,
(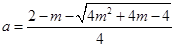 (负根舍去)),
(负根舍去)),
函数 有一零点
有一零点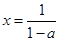 . 10分
. 10分
ii) 当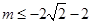 时,
时,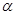 的两根都为正数,
的两根都为正数,
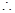 当
当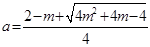 或
或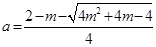 时,
时,
函数 有一零点
有一零点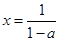 .
11分
.
11分
ⅲ) 当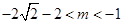 时,
时,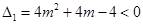 ,∴
,∴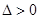
③方程(※)有二解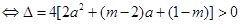 ,
,
ⅰ)若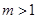 ,
,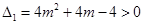 ,
,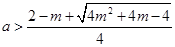 时,
时,
(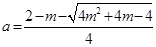 (负根舍去)),函数
(负根舍去)),函数
有两个零点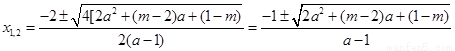 ;
12分
;
12分
ⅱ)当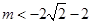 时,
时,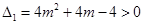 ,
,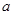 的两根都为正数,
的两根都为正数,
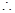 当
当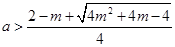 或
或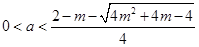 时,
时,
函数 有两个零点
有两个零点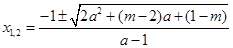 . 13分
. 13分
ⅲ) 当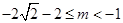 时,
时,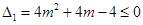 ,∴
,∴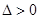 恒成立,
恒成立,
∴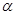 取大于0(
取大于0(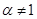 )的任意数,
)的任意数,
函数 有两个零点
有两个零点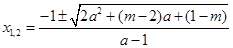 14分
14分
考点:1.函数解析式的求法;2.二次函数最小值的求法;3.分式不等式的解法;4.含参方程的解法.

 字词句段篇系列答案
字词句段篇系列答案 满足
满足 ,
, ;方程
;方程 有两个实根,且两实根的平方和为10.
有两个实根,且两实根的平方和为10. 的方程
的方程 在区间
在区间 内有两个不等实根,求实数
内有两个不等实根,求实数 的取值范围.
的取值范围.