题目内容
10.已知sin(2x+$\frac{π}{3}$)=$\frac{1}{2}$,x∈(-$\frac{π}{6}$,$\frac{π}{3}$),求角x.分析 由题意可得2x+$\frac{π}{3}$∈(0,π),结合sin(2x+$\frac{π}{3}$)=$\frac{1}{2}$可得2x+$\frac{π}{3}$=$\frac{π}{6}$或$\frac{5π}{6}$,解方程可得.
解答 解:∵x∈(-$\frac{π}{6}$,$\frac{π}{3}$),∴2x+$\frac{π}{3}$∈(0,π),
∵sin(2x+$\frac{π}{3}$)=$\frac{1}{2}$,∴2x+$\frac{π}{3}$=$\frac{π}{6}$或$\frac{5π}{6}$,
解得x=-$\frac{π}{12}$或x=$\frac{π}{4}$.
点评 本题考查三角函数求值,涉及正弦函数的单调性和特殊值,属基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.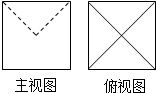 某几何体正视图与侧视图相同,其正视图与俯视图如图所示,且图中的四边形都是边长为2的正方形,正视图中两条虚线互相垂直,则该几何体的表面积是( )
某几何体正视图与侧视图相同,其正视图与俯视图如图所示,且图中的四边形都是边长为2的正方形,正视图中两条虚线互相垂直,则该几何体的表面积是( )
 某几何体正视图与侧视图相同,其正视图与俯视图如图所示,且图中的四边形都是边长为2的正方形,正视图中两条虚线互相垂直,则该几何体的表面积是( )
某几何体正视图与侧视图相同,其正视图与俯视图如图所示,且图中的四边形都是边长为2的正方形,正视图中两条虚线互相垂直,则该几何体的表面积是( )| A. | 24 | B. | 20+4$\sqrt{2}$ | C. | 24+4$\sqrt{2}$ | D. | 20+4$\sqrt{3}$ |