题目内容
设M是线段BC的中点,点A在直线BC外,
2=16,|
+
|=|
-
|,则|
|=
| BC |
| AB |
| AC |
| AB |
| AC |
| AM |
2
2
.分析:根据向量加法的平行四边形形法则和减法的三角形法则,可得以AB、AC为邻边的平行四边形ABDC为矩形,可得AM是Rt△ABC斜边BC上的中线,可得|
|=
|
|,结合题中数据即可算出|
|的值.
| AM |
| 1 |
| 2 |
| BC |
| AM |
解答:解:∵|
+
|=|
-
|
∴以AB、AC为邻边作平行四边形,可得对角线AD与BC长度相等
因此,四边形ABDC为矩形
∵M是线段BC的中点,
∴AM是Rt△ABC斜边BC上的中线,可得|
|=
|
|
∵
2=16,得|
|2=16,即|
|=4
∴|
|=
|
|=2
故答案为:2
| AB |
| AC |
| AB |
| AC |

∴以AB、AC为邻边作平行四边形,可得对角线AD与BC长度相等
因此,四边形ABDC为矩形
∵M是线段BC的中点,
∴AM是Rt△ABC斜边BC上的中线,可得|
| AM |
| 1 |
| 2 |
| BC |
∵
| BC |
| BC |
| BC |
∴|
| AM |
| 1 |
| 2 |
| BC |
故答案为:2
点评:本题给出向量
、
满足的等式和向量
的模,求另一个向量的模.着重考查了向量的加法、减法法则和模的计算公式等知识,属于基础题.
| AB |
| AC |
| BC |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 设A、B为函数
设A、B为函数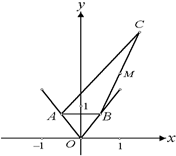 设A、B为函数
设A、B为函数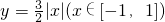 图象上不同的两个点,且 AB∥x轴,又有定点
图象上不同的两个点,且 AB∥x轴,又有定点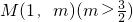 ,已知M是线段BC的中点.
,已知M是线段BC的中点. 设A、B为函数
设A、B为函数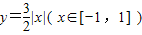 图象上不同的两个点,且 AB∥x轴,又有定点
图象上不同的两个点,且 AB∥x轴,又有定点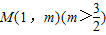 ,已知M是线段BC的中点.
,已知M是线段BC的中点.