题目内容
将边长为a的正方形ABCD沿对角线AC折起,折后连接BD,构成三棱锥D-ABC,若棱BD的长为 a.则此时三棱锥D-ABC的体积是
a.则此时三棱锥D-ABC的体积是
- A.
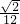 a3
a3 - B.
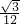 a3
a3 - C.
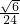 a3
a3 - D.
 a3
a3
C
分析:如图,由正方形的性质可以求得其对角线长度是 a,折起后的图形中,DE=BE=
a,折起后的图形中,DE=BE= a,又知BD=
a,又知BD= a,由此知三角形BDE为正三角形,解出三角形BDE的面积,
a,由此知三角形BDE为正三角形,解出三角形BDE的面积,
又可证得三棱锥D-ABC的体积可看作面BDE为底,高分别为AE,EC的两个棱锥的体积和,从而可解.
解答: 解:如图,
解:如图,
由题意知DE=BE= a,BD=
a,BD= a,
a,
则△DEB为正三角形,
故三角形BDE面积是 ×(
×( a)2=
a)2= a2,
a2,
又正方形的对角线互相垂直,且翻折后,AC与DE,BE仍然垂直,故AE,CE分别是以面BDE为底的两个三棱锥的高,
故三棱锥D-ABC的体积为 ×
× a×
a× a2=
a2=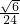 a3,
a3,
故选C.
点评:本题考查棱柱、棱锥、棱台的体积,解题的关键是正确理解图形,将求几何体体积变为求两个几何体的体积,换一个角度求解,使得解题过程变得容易.
分析:如图,由正方形的性质可以求得其对角线长度是
 a,折起后的图形中,DE=BE=
a,折起后的图形中,DE=BE= a,又知BD=
a,又知BD= a,由此知三角形BDE为正三角形,解出三角形BDE的面积,
a,由此知三角形BDE为正三角形,解出三角形BDE的面积,又可证得三棱锥D-ABC的体积可看作面BDE为底,高分别为AE,EC的两个棱锥的体积和,从而可解.
解答:
 解:如图,
解:如图,由题意知DE=BE=
 a,BD=
a,BD= a,
a,则△DEB为正三角形,
故三角形BDE面积是
 ×(
×( a)2=
a)2= a2,
a2,又正方形的对角线互相垂直,且翻折后,AC与DE,BE仍然垂直,故AE,CE分别是以面BDE为底的两个三棱锥的高,
故三棱锥D-ABC的体积为
 ×
× a×
a× a2=
a2=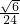 a3,
a3,故选C.
点评:本题考查棱柱、棱锥、棱台的体积,解题的关键是正确理解图形,将求几何体体积变为求两个几何体的体积,换一个角度求解,使得解题过程变得容易.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
相关题目
将边长为a的正方形ABCD沿对角线AC折起,使得BD=a,则三棱锥D-ABC的体积为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,将边长为a的正方形剪去阴影部分后,围成一个正三棱锥,则正三棱锥的体积是
如图,将边长为a的正方形剪去阴影部分后,围成一个正三棱锥,则正三棱锥的体积是 如图,将边长为3的正方形ABCD绕中心O顺时针旋转α (0<α<
如图,将边长为3的正方形ABCD绕中心O顺时针旋转α (0<α<