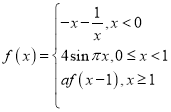题目内容
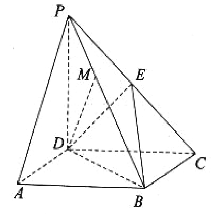
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是平行四边形,
是平行四边形,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() 是棱
是棱![]() 上的一点.
上的一点.
(1)若![]() 平面
平面![]() ,证明:
,证明:![]() ;
;
(2)在(1)的条件下,棱![]() 上是否存在点
上是否存在点![]() ,使直线
,使直线![]() 与平面
与平面![]() 所成角的大小为
所成角的大小为![]() ?若存在,求
?若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1) 见解析;(2)在棱![]() 上存在点
上存在点![]() 使直线
使直线![]() 与平面
与平面![]() 所成角的大小为
所成角的大小为![]() ,此时
,此时![]() .
.
【解析】
(1)连接![]() 交
交![]() 于
于![]() ,连接
,连接![]() 由
由![]() 平面
平面![]() 的性质定理得
的性质定理得![]() 是
是![]() 的中点,即可得出;(2)建立空间直角坐标系,求出平面
的中点,即可得出;(2)建立空间直角坐标系,求出平面![]() 的法向量,由直线
的法向量,由直线![]() 与平面
与平面![]() 所成角的向量法,得出
所成角的向量法,得出![]() 的值.
的值.

(1)连接![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,则
,则![]() 是平面
是平面![]() 与平面
与平面![]() 的交线.因为
的交线.因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() .又因为
.又因为![]() 是
是![]() 中点,所以
中点,所以![]() 是
是![]() 的中点.所以
的中点.所以![]() .
.
(2)由已知条件可知![]() ,所以
,所以![]() ,
,
以![]() 为原点,
为原点,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴建立空间直角坐标系.
轴建立空间直角坐标系.
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() .
.
假设在棱![]() 上存在点
上存在点![]() ,设
,设![]() ,
,
得![]() ,
,![]() .
.
记平面![]() 的法向量为
的法向量为![]() ,则
,则

即![]() 取
取![]() ,则
,则![]() ,
,
所以![]() .
.
要使直线![]() 与平面
与平面![]() 所成角的大小为
所成角的大小为![]() ,
,
则 ,即
,即![]() ,解得
,解得![]() .
.
所以在棱![]() 上存在点
上存在点![]() 使直线
使直线![]() 与平面
与平面![]() 所成角的大小为
所成角的大小为![]() .
.
此时![]() .
.

 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案【题目】“中国大能手”是央视推出的一档大型职业技能挑战赛类节目,旨在通过该节目,在全社会传播和弘扬“劳动光荣、技能宝贵、创造伟大”的时代风尚.某公司准备派出选手代表公司参加“中国大能手”职业技能挑战赛.经过层层选拔,最后集中在甲、乙两位选手在一项关键技能的区分上,选手完成该项挑战的时间越少越好.已知这两位选手在15次挑战训练中,完成该项关键技能挑战所用的时间(单位:秒)及挑战失败(用“×”表示)的情况如下表1:
序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
甲 | × | 96 | 93 | × | 92 | × | 90 | 86 | × | × | 83 | 80 | 78 | 77 | 75 |
乙 | × | 95 | × | 93 | × | 92 | × | 88 | 83 | × | 82 | 80 | 80 | 74 | 73 |
据表1中甲、乙两选手完成该项关键技能挑战成功所用时间的数据,应用统计软件得下表2:
数字特征 | 均值(单位:秒)方差 | 方差 |
甲 | 85 | 50.2 |
乙 | 84 | 54 |
(1)在表1中,从选手甲完成挑战用时低于90秒的成绩中,任取2个,求这2个成绩都低于80秒的概率;
(2)若该公司只有一个参赛名额,以该关键技能挑战成绩为标准,根据以上信息,判断哪位选手代表公司参加职业技能挑战赛更合适?请说明你的理由.
【题目】在![]() 年
年![]() 月
月![]() 日,某市物价部门对本市的
日,某市物价部门对本市的![]() 家商场的某商品的一天销售量及其价格进行调查,
家商场的某商品的一天销售量及其价格进行调查,![]() 家商场的售价
家商场的售价![]() 元和销售量
元和销售量![]() 件之间的一组数据如表所示:
件之间的一组数据如表所示:
价格 | 9 | 9.5 | 10 | 10.5 | 11 |
销售量 | 11 | 10 | 8 | 6 | 5 |
根据公式计算得相关系数![]() ,其线性回归直线方程是:
,其线性回归直线方程是:![]() ,则下列说法正确的有( )
,则下列说法正确的有( )
参考:![]()
A.有![]() 的把握认为变量
的把握认为变量![]() 具有线性相关关系
具有线性相关关系
B.回归直线恒过定点![]()
C.![]()
D.当![]() 时,
时,![]() 的估计值为
的估计值为![]()
【题目】某同学用“五点法”画函数![]() ,在某一周期内的图象时,列表并填入了部分数据,如下表:
,在某一周期内的图象时,列表并填入了部分数据,如下表:
| 0 |
|
|
|
|
x |
|
| |||
| 0 | 2 | 0 | 0 |
(1)请将上表数据补充完整,并求函数![]() 的解析式;
的解析式;
(2)求函数![]() 的单调递增区间;
的单调递增区间;
(3)求函数![]() 在区间
在区间![]() 上的最大值和最小值.
上的最大值和最小值.