题目内容
设a∈R,向量m=(a,1),函数y=f(x)的图象经过坐标原点,f′(x)是函数f(x)的导函数.已知A(-1,f′(-1)),B(x,x2),f′(x)= m.
m.(Ⅰ)求f(x)的解析式;
(Ⅱ)若方程
 在区间[-1,1]上有两个不相等的实数根,求a的取值范围;
在区间[-1,1]上有两个不相等的实数根,求a的取值范围;(Ⅲ)若a=2,设数列{an}满足a1=3,4an=2f'(an-1)-3(n=2,3,4,…).求证:
 (n∈N*).
(n∈N*).
【答案】分析:(I)由题设知 ,
, m=a(x+1)+x2-f'(-1).
m=a(x+1)+x2-f'(-1). .由y=f(x)的图象过原点,知
.由y=f(x)的图象过原点,知 .
.
(II)原方程整理为 .令
.令 ,则g'(x)=2x2+x-1.再由函数的增减性知要使原方程在[-1,1]上有两个不相等的实数根,则须使
,则g'(x)=2x2+x-1.再由函数的增减性知要使原方程在[-1,1]上有两个不相等的实数根,则须使 ≤
≤ .从而得到a的取值范围.
.从而得到a的取值范围.
(III)a=2时, .所以(an-1+1)2=2an+1<2(an+1),令cn=an+1,则c1=4,2cn>cn-12(n≥2).然后两边同时取对数,再结合题设条件进行求解.
.所以(an-1+1)2=2an+1<2(an+1),令cn=an+1,则c1=4,2cn>cn-12(n≥2).然后两边同时取对数,再结合题设条件进行求解.
解答:解:(I)∵ ,
,
∴ m=a(x+1)+x2-f'(-1).
m=a(x+1)+x2-f'(-1).
令x=-1,则f'(-1)=a(x+1)+(-1)2-f'(-1),解得 .
.
∴ .
.
∵y=f(x)的图象过原点,
∴ .(4分)
.(4分)
(II)原方程可以整理为 .
.
令 ,则g'(x)=2x2+x-1.
,则g'(x)=2x2+x-1.
由g'(x)=0有x=-1或 ,
,
且当x<-1或 时g'(x)>0,当
时g'(x)>0,当 时g'(x)<0.
时g'(x)<0.
∴在x∈[-1,1]时,g(x)在[-1, ]上是减函数,在[
]上是减函数,在[ ,1]上是增函数,(8分)
,1]上是增函数,(8分)
∴在[-1,1]上 .
.
又 >
> ,
,
∴要使原方程在[-1,1]上有两个不相等的实数根,则须使 ≤
≤ .
.
即a的取值范围为 .(10分)
.(10分)
(III)a=2时, .
.
∴4an=2( )-3,整理得2an=an-12+2an-1(n≥2).
)-3,整理得2an=an-12+2an-1(n≥2).
变形得(an-1+1)2=2an+1<2(an+1),
令cn=an+1,则c1=4,2cn>cn-12(n≥2).
两边同取对数有log2(2cn)>log2cn-12,即1+log2cn>2log2cn-1.
令dn=log2cn,则d1=2,且1+dn>2dn-1,
∴dn-1>2(dn-1-1)(n≥2),
∴dn-1>2(dn-1-1)>22(dn-2-1)>>2n-1(d1-1)=2n-1,
∴dn>1+2n-1>2n-1,
∴cn= >
> ,
,
∴an> -1(n≥2).
-1(n≥2).
当n=1时,a1=3> -1=1,即不等式也成立,
-1=1,即不等式也成立,
∴an> -1(n∈N*).(14分)
-1(n∈N*).(14分)
点评:本题考查数列和不等式的合理运用,解题时要认真审题,仔细解答,注意公式的灵活运用.
 ,
, m=a(x+1)+x2-f'(-1).
m=a(x+1)+x2-f'(-1). .由y=f(x)的图象过原点,知
.由y=f(x)的图象过原点,知 .
.(II)原方程整理为
 .令
.令 ,则g'(x)=2x2+x-1.再由函数的增减性知要使原方程在[-1,1]上有两个不相等的实数根,则须使
,则g'(x)=2x2+x-1.再由函数的增减性知要使原方程在[-1,1]上有两个不相等的实数根,则须使 ≤
≤ .从而得到a的取值范围.
.从而得到a的取值范围.(III)a=2时,
 .所以(an-1+1)2=2an+1<2(an+1),令cn=an+1,则c1=4,2cn>cn-12(n≥2).然后两边同时取对数,再结合题设条件进行求解.
.所以(an-1+1)2=2an+1<2(an+1),令cn=an+1,则c1=4,2cn>cn-12(n≥2).然后两边同时取对数,再结合题设条件进行求解.解答:解:(I)∵
 ,
,∴
 m=a(x+1)+x2-f'(-1).
m=a(x+1)+x2-f'(-1).令x=-1,则f'(-1)=a(x+1)+(-1)2-f'(-1),解得
 .
.∴
 .
.∵y=f(x)的图象过原点,
∴
 .(4分)
.(4分)(II)原方程可以整理为
 .
.令
 ,则g'(x)=2x2+x-1.
,则g'(x)=2x2+x-1.由g'(x)=0有x=-1或
 ,
,且当x<-1或
 时g'(x)>0,当
时g'(x)>0,当 时g'(x)<0.
时g'(x)<0.∴在x∈[-1,1]时,g(x)在[-1,
 ]上是减函数,在[
]上是减函数,在[ ,1]上是增函数,(8分)
,1]上是增函数,(8分)∴在[-1,1]上
 .
.又
 >
> ,
,∴要使原方程在[-1,1]上有两个不相等的实数根,则须使
 ≤
≤ .
.即a的取值范围为
 .(10分)
.(10分)(III)a=2时,
 .
.∴4an=2(
 )-3,整理得2an=an-12+2an-1(n≥2).
)-3,整理得2an=an-12+2an-1(n≥2).变形得(an-1+1)2=2an+1<2(an+1),
令cn=an+1,则c1=4,2cn>cn-12(n≥2).
两边同取对数有log2(2cn)>log2cn-12,即1+log2cn>2log2cn-1.
令dn=log2cn,则d1=2,且1+dn>2dn-1,
∴dn-1>2(dn-1-1)(n≥2),
∴dn-1>2(dn-1-1)>22(dn-2-1)>>2n-1(d1-1)=2n-1,
∴dn>1+2n-1>2n-1,
∴cn=
 >
> ,
,∴an>
 -1(n≥2).
-1(n≥2).当n=1时,a1=3>
 -1=1,即不等式也成立,
-1=1,即不等式也成立,∴an>
 -1(n∈N*).(14分)
-1(n∈N*).(14分)点评:本题考查数列和不等式的合理运用,解题时要认真审题,仔细解答,注意公式的灵活运用.

练习册系列答案
相关题目
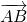 m.
m.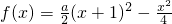 在区间[-1,1]上有两个不相等的实数根,求a的取值范围;
在区间[-1,1]上有两个不相等的实数根,求a的取值范围;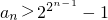 (n∈N*).
(n∈N*).