题目内容
(本小题12分)定义运算:
(1)若已知 ,解关于
,解关于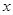 的不等式
的不等式
(2)若已知 ,对任意
,对任意 ,都有
,都有 ,求实数
,求实数 的取值范围。
的取值范围。
【答案】
((1) ;(2)
;(2) .
.
【解析】
试题分析:(1)当 时,根据定义有
时,根据定义有

所以原不等式的解集为

(2)依题意知

因为对任意 ,都有
,都有 ,
,
所以
因为 的图像开口向下,对称轴为直线
的图像开口向下,对称轴为直线

①
若 ,即
,即 ,则
,则 在
在 为减函数,
为减函数,
所以 ,解得
,解得 ,所以
,所以

②
若 ,即
,即 ,则
,则 ,
,
解得 ,所以
,所以

③
若 ,即
,即 ,则
,则 在
在 为增函数,
为增函数,
所以 ,解得
,解得 ,所以
,所以

综上所述,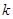 的取值范围是
的取值范围是

考点:本题主要以新定义为背景,考查恒成立问题.
点评:对于此类新定义问题,学生要注意仔细审题,冷静思考,新问题的解决还是要靠“老知识”“老方法”,应该有意识地运用转化思想,将新问题转化为我们熟知的问题。对于恒成立问题,要转为为求最值来解决,分情况讨论求最值时,要做到不重不漏.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 是定义在
是定义在 上的偶函数,已知
上的偶函数,已知 时,
时, .
.
 ,
, 的奇偶性并用定义证明;
的奇偶性并用定义证明; 时,总有
时,总有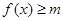 成立,求
成立,求 的取值范围.
的取值范围. 对称,求b的最小值.
对称,求b的最小值. ,若对任意的
,若对任意的 都有
都有 ,则称函数
,则称函数 为“妈祖函数”,否则称“非妈祖函数”.试问函数
为“妈祖函数”,否则称“非妈祖函数”.试问函数 ,
, )是否为“妈祖函数”?如果是,请给出证明;如果不是,请说明理由.
)是否为“妈祖函数”?如果是,请给出证明;如果不是,请说明理由.
