Question

如图，已知三角形PAQ顶点P(－3，0)，点A在y轴上，点Q在x轴正半轴上，·＝0，＝2．

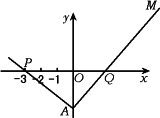
(1)当点A在y轴上移动时，求动点M的轨迹E的方程；

(2)设直线l：y＝k(x＋1)与轨迹E交于B、C两点，点D(1，0)，若∠BDC为钝角，求k的取值范围．

Answer 1

答案：
解析：

解：(1)设＝(x，y)，＝(0，a)，＝(b，0)(b＞0) 　　则＝(3，a)，＝(b，－a)，又·＝0， 　　∴a2＝3b　　　　① 　　又∵＝(x－b，y)，＝(b，－a)，＝2， 　　∴　　　　② 　　由①②得y2＝4x(x≠0) 　　(2)设＝(x1，y1)，＝(x2，y2)，＝(x1－1，y1) 　　＝(x2－1，y2)，·＝||·||cos∠BDC， 　　∵∠BDC为钝角，∴cos∠BDC＝＜0， 　　∴·＜0， 　　∴x1x2－(x1＋x2)＋1＋y1y2＜0　　　　③ 　　由消去y得：k2x2＋(2k2－4)x＋k2＝0(k≠0)，则 　　x1＋x2＝，x1x2＝1　　　　④ 　　y1y2＝k2(x1＋1)(x2＋1)＝k2[x1x2＋(x1＋x2)＋1]　　　　⑤ 　　④⑤代入③，得k2＜－＜k＜．(k≠0)，满足Δ＞0．