题目内容
【题目】已知函数![]() ,曲线
,曲线![]() 在
在![]() 处的切线方程为
处的切线方程为![]() .
.
(1)求![]() 的值;
的值;
(2)求证:![]() 时,
时,![]() ;
;
(3)求证:![]() .
.
【答案】见解析.
【解析】分析:第一问对函数求导,求得![]() 的值,紧接着求得
的值,紧接着求得![]() ,从而应用点斜式求得直线的方程,与题中所给的直线方程对比,求得参数
,从而应用点斜式求得直线的方程,与题中所给的直线方程对比,求得参数![]() 的值,第二问将所求的
的值,第二问将所求的![]() 的值代入,之后构造新函数,利用导数得到函数的单调性,之后证得结果,第三问借助于第二问所证得的不等式,将其中变量加以代换,之后对不等式进行变形,并且对其进行适当的放缩,然后应用裂项相消法求和,证得结果.
的值代入,之后构造新函数,利用导数得到函数的单调性,之后证得结果,第三问借助于第二问所证得的不等式,将其中变量加以代换,之后对不等式进行变形,并且对其进行适当的放缩,然后应用裂项相消法求和,证得结果.
详解:(Ⅰ)函数![]() 定义域为
定义域为![]() ,
,![]() ,
,![]()
又因为![]()
所以该切线方程为![]() ,即
,即![]() ,
,![]() .
.
(2)设![]() ,
,
则![]()
设![]() ,
,![]()
则![]()
当![]() ,
,![]() ,又
,又![]() ,故
,故![]()
所以![]() ,即
,即![]() 在区间
在区间![]() 上单调递增,所以
上单调递增,所以![]()
所以![]() ,
,![]()
(2)由(2)可知,![]()
令![]() ,则
,则![]() ,
,
因为![]()
所以![]() 时,有
时,有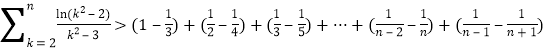
化简为 ,
,
即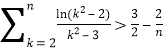 ,所以
,所以 .
.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案
相关题目