题目内容
设 ,函数
,函数 .
.
(I)当 时,求
时,求 的极小值;
的极小值;
(II)设 ,若对于任意的
,若对于任意的 ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(1)当 时,函数
时,函数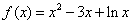 ,则
,则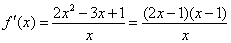 .
.
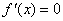 得:
得: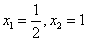 ;令
;令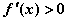 得
得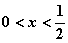 或
或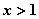 ;令
;令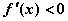 得
得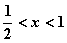 ,所以
,所以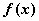 的单调递增区间为
的单调递增区间为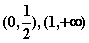 ,单调递减区间为
,单调递减区间为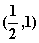
因此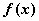 的极小值为
的极小值为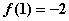 …………5分
…………5分
(2)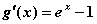 ,易知
,易知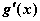 在
在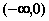 单调递减,在
单调递减,在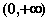 单调递增,
单调递增,
所以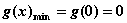 , …………7分
, …………7分
对于任意的 ,不等式
,不等式 恒成立,
恒成立,
也即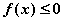 对任意的
对任意的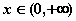 恒成立, …………8分
恒成立, …………8分
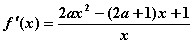 ,(x>0)
,(x>0)
①当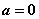 时,
时,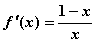 ,易知
,易知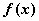 在
在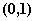 单调增,在
单调增,在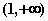 单调减,
单调减,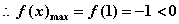 ,所以
,所以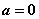 符合题意; …………9分
符合题意; …………9分
②当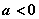 时,
时,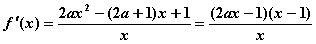
令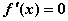 得
得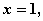 ,易知
,易知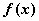 在
在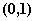 单调增,在
单调增,在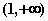 单调减,
单调减,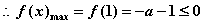 ,得
,得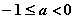 ,所以
,所以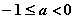 符合题意
符合题意
………10分
③当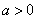 时,
时,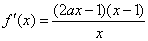 ,
,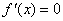 得
得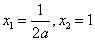
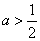 时,
时,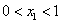 ,
,
解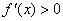 得
得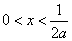 或
或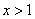 ;解
;解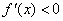 得
得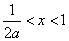
所以 在
在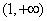 是增函数,
是增函数,
而当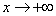 时,
时,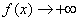 ,这与对于任意的
,这与对于任意的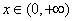 时
时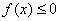 矛盾
矛盾
同理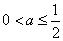 时也不成立. …………11分
时也不成立. …………11分
综上所述, 的取值范围为
的取值范围为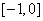 .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
下面有三个游戏规则,袋子中分别装有球,从袋中无放回地取球,问其中不公平的游戏是( )
| 游戏 | 游戏 | 游戏 |
|
|
|
|
| 取 | 取 | 取 |
| 取出的两个球同色→甲胜 | 取出的球是黑球→甲胜 | 取出的两个球同色→甲胜 |
| 取出的两个球不同色→乙胜 | 取出的球是白球→乙胜 | 取出的两个球不同色→乙胜 |
A. 游戏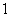 B.游戏
B.游戏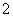 C.游戏
C.游戏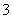 D.游戏
D.游戏 和游戏
和游戏

 满足
满足 (其中
(其中 ),q:实数x满足
),q:实数x满足
 ,且p∧q为真,求实数
,且p∧q为真,求实数 的取值范围.
的取值范围.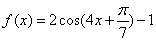 与函数
与函数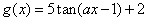 的最小正周期相同,则实数a= .
的最小正周期相同,则实数a= .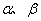 的顶点在坐标原点,始边与x轴的正半轴重合,
的顶点在坐标原点,始边与x轴的正半轴重合,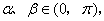 角
角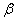 的终边与单位圆交点的横坐标是
的终边与单位圆交点的横坐标是 ,角
,角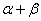 的终边与单位圆交点的纵坐标是
的终边与单位圆交点的纵坐标是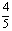 ,则
,则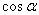 = .
= .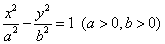 的一个焦点是
的一个焦点是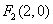 ,且
,且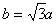 .
.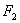 的直线
的直线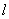 的一个法向量为
的一个法向量为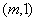 ,当直线
,当直线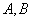 不同的两点时,求实数
不同的两点时,求实数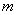 的取值范围;并证明
的取值范围;并证明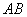 中点
中点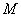 在曲线
在曲线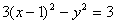 上.
上.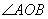 为锐角?若存在,请求出
为锐角?若存在,请求出 cm,半径为
cm,半径为 cm,则该圆锥的体积等于
cm,则该圆锥的体积等于  .
.