题目内容
【题目】已知数列![]() 满足:①
满足:①![]() (
(![]() );②当
);②当![]() (
(![]() )时,
)时,![]() ;③当
;③当![]() (
(![]() )时,
)时,![]() ,记数列
,记数列![]() 的前
的前![]() 项和为
项和为![]() .
.
(1)求![]() ,
,![]() ,
,![]() 的值;
的值;
(2)若![]() ,求
,求![]() 的最小值;
的最小值;
(3)求证:![]() 的充要条件是
的充要条件是![]() (
(![]() ).
).
【答案】(1)![]() ,
,![]() 或1,
或1,![]() 或1;(2)115;(3)证明见解析.
或1;(2)115;(3)证明见解析.
【解析】
(1)先根据题中条件,求出![]() ,
,![]() ,
,![]() ,再结合题意,即可得出结果;
,再结合题意,即可得出结果;
(2)先由题意,得到![]() ,当
,当![]()
![]() 时,
时,![]() ,由于
,由于![]() ,所以
,所以![]() 或
或![]() ,
,![]() 分别求出
分别求出![]() ,
,![]() ,进而可求出结果;
,进而可求出结果;
(3)先由![]() ,根据题中条件,求出
,根据题中条件,求出![]() ,证明必要性;再由
,证明必要性;再由![]() ,求出
,求出![]() ,证明充分性即可.
,证明充分性即可.
(1)因![]() ,
,![]() ,且
,且![]() 是自然数,
是自然数,![]() ;
;
![]() ,
,![]() ,且
,且![]() 都是自然数;
都是自然数;![]()
![]() 或
或![]() ;
;
![]() ,
,![]() ,且
,且![]() ,
,![]()
![]() 或
或![]() .
.
(2)由题意可得:![]() ,当
,当![]()
![]() 时,
时,
![]() ,由于
,由于![]() ,
,
所以![]() 或
或![]() ,
,![]()
![]()
![]()
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
又![]() ,
,
![]()
所以![]()
(3)必要性:若![]() ,
,
则:![]() ①
①
![]() ②
②
①![]() ②得:
②得:![]() ③
③
由于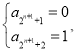 或
或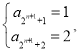 或
或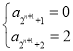 ,且
,且![]() 或
或![]()
只有当![]() 同时成立时,等式③才成立,
同时成立时,等式③才成立,
![]() ;
;
充分性:若![]() ,由于
,由于![]()
所以![]() ,
,
即![]() ,
,![]() ,
,![]() ,…,
,…,![]() ,又
,又![]()
所以对任意的![]() ,都有
,都有![]() …(I)
…(I)
另一方面,由![]() ,
,![]()
![]()
所以对任意的![]() ,都有
,都有![]() …(II)
…(II)
![]()
![]() ,
,
由于![]()
![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】某小店每天以每份5元的价格从食品厂购进若干份食品,然后以每份10元的价格出售.如果当天卖不完,剩下的食品还可以每份1元的价格退回食品厂处理.
(Ⅰ)若小店一天购进16份,求当天的利润![]() (单位:元)关于当天需求量
(单位:元)关于当天需求量![]() (单位:份,
(单位:份,![]() )的函数解析式;
)的函数解析式;
(Ⅱ)小店记录了100天这种食品的日需求量(单位:份),整理得下表:
日需求量 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
频数 | 10 | 20 | 16 | 16 | 15 | 13 | 10 |
以100天记录的各需求量的频率作为各需求量发生的概率.
(i)小店一天购进16份这种食品,![]() 表示当天的利润(单位:元),求
表示当天的利润(单位:元),求![]() 的分布列及数学期望;
的分布列及数学期望;
(ii)以小店当天利润的期望值为决策依据,你认为一天应购进食品16份还是17份?