题目内容

已知方程x2-(bcosA)x+acosB=0的两根之积等于两根之和,且a、b为△ABC的两边,A、B为两内角,试判定这个三角形的形状.

答案：解法一:设方程的两根为x1、x2,由韦达定理知:

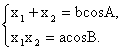由题意有bcosA=acosB.

根据余弦定理得

b·=a·,

∴b2+c2-a2=a2+c2-b2.

化简得a=b.

∴△ABC为等腰三角形.

解法二:仿解法一得：bcosA=acosB，

由正弦定理得

2RsinBcosA=2RsinAcosB，

∴sinAcosB-cosAsinB=0,

即sin(A-B)=0.

∵A、B为△ABC内角,∴0＜A＜π,0＜B＜π.∴A-B=0,即A=B,

故△ABC为等腰三角形.

练习册系列答案
相关题目
已知圆x2+y2=1，点A（1，0），△ABC内接于圆，且∠BAC=60°，当B、C在圆上运动时，BC中点的轨迹方程是（　　）
A、x2+y2=
1
2
B、x2+y2=
1
4
C、x2+y2=
1
2
（x＜
1
2
）
D、x2+y2=
1
4
（x＜
1
4
）
已知圆x2+y2=25，△ABC内接于此圆，A点的坐标（3，4），O为坐标原点．
（1）若△ABC的重心是G(
53
，2)，求直线BC的方程；（三角形重心是三角形三条中线的交点，并且重心到顶点的距离是它到对边中点距离的两倍）
（2）若直线AB与直线AC的倾斜角互补，求证：直线BC的斜率为定值．
已知抛物线x2=4y的焦点为F，过F任作直线l（l与x轴不平行）交抛物线分别于A，B两点，点A关于y轴对称点为C，
（1）求证：直线BC与y轴交点D必为定点；
（2）过A，B分别作抛物线的切线，两条切线交于E，求
|AB|
|DE|
的最小值，并求当
|AB|
|DE|
取最小值时直线l的方程．
已知半圆x2+y2=4（y≥0），动圆与此半圆相切且与x轴相切．
（1）求动圆圆心的轨迹，并画出其轨迹图形．
（2）是否存在斜率为
13
的直线l，它与（1）中所得轨迹的曲线由左到右顺次交于A、B、C、D四点，且满足|AD=2|BC|．若存在，求出l的方程；若不存在，说明理由．
（2013•枣庄二模）已知抛物线x2=2py上点（2，2）处的切线经过椭圆E：
y2
a2
+
x2
b2
=1(a＞b＞0)的两个顶点．
（1）求椭圆E的方程；
（2）过椭圆E的上顶点A的两条斜率之积为-4的直线与该椭圆交于B、C两点．请问：是否存在一点D，使得直线BC恒过该点？若存在，请求出定点D的坐标；若不存在，请说明理由；
（3）在（2）的条件下，过点A作直线BC的垂线，垂足为H，求点H的轨迹方程．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网