题目内容
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是矩形,AD⊥PD,BC=1,PC=2 ![]() ,PD=CD=2,则二面角A﹣PB﹣C的正切值为 .
,PD=CD=2,则二面角A﹣PB﹣C的正切值为 . 
【答案】![]()
【解析】解:以D为原点,DA为x轴,DC为y轴,过D作平面ABCD的垂直线为z轴,建立空间直角坐标系,

在△PDC中,由于PD=CD=2,PC=2 ![]() ,可得∠PCD=30°,
,可得∠PCD=30°,
∴P到平面ABCD的距离为PCsin30°= ![]() .
.
∴A(1,0,0),P(0,﹣1, ![]() ),B(1,2,0),C(0,2,0),
),B(1,2,0),C(0,2,0),
![]() =(1,1,﹣
=(1,1,﹣ ![]() ),
), ![]() =(1,3,﹣
=(1,3,﹣ ![]() ),
), ![]() =(0,3,﹣
=(0,3,﹣ ![]() ),
),
设平面PAB的法向量 ![]() =(x,y,z),
=(x,y,z),
则  ,取z=1,得
,取z=1,得 ![]() =(
=( ![]() ),
),
设平面PBC的法向量 ![]() =(a,b,c),
=(a,b,c),
则 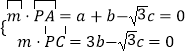 ,取c=
,取c= ![]() ,得
,得 ![]() =(2,1,
=(2,1, ![]() ),
),
设二面角A﹣PB﹣C的平面角为θ,
则cosθ= ![]() =
= ![]() =
= ![]() ,sinθ=
,sinθ= ![]() =
= ![]() ,
,
tanθ= ![]() =
= ![]() .
.
∴二面角A﹣PB﹣C的正切值为 ![]() .
.
故答案为: ![]() .
.
以D为原点,DA为x轴,DC为y轴,过D作平面ABCD的垂直线为z轴,建立空间直角坐标系,利用向量法能求出二面角A﹣PB﹣C的正切值.

练习册系列答案
相关题目
【题目】东莞某家具生产厂家根据市场调查分析,决定调整新产品生产方案,准备每周(按40个工时计算)生产书桌、书柜、电脑椅共120张,且书桌至少生产20张.已知生产这些家具每张所需工时和每张产值如表:
家具名称 | 书桌 | 书柜 | 电脑椅 |
工 时 |
|
|
|
产值(千元) | 4 | 3 | 2 |
问每周应生产书桌、书柜、电脑椅各多少张,才能使产值最高?最高产值是多少?(以千元为单位)