题目内容
已知函数 ,则f(x)
,则f(x)
- A.在(-2,+∞)上是增函数
- B.在(-2,+∞)上是减函数
- C.在(2,+∞)上是增函数
- D.在(2,+∞)上是减函数
D
分析:根据函数f(x)= 的性质来类比函数
的性质来类比函数 ,从而求解;
,从而求解;
解答:∵函数 ,类比y═
,类比y═ 的单调性,我们知道,
的单调性,我们知道,
∴当x-2>0时即x>2,f(x)=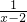 为减函数;
为减函数;
当x-2<0时即x<2,f(x)=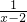 为减函数;
为减函数;
故选D.
点评:此题主要考查函数的单调性的判断与证明,此题用类比法,此题是一道基础题.
分析:根据函数f(x)=
 的性质来类比函数
的性质来类比函数 ,从而求解;
,从而求解;解答:∵函数
 ,类比y═
,类比y═ 的单调性,我们知道,
的单调性,我们知道,∴当x-2>0时即x>2,f(x)=
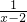 为减函数;
为减函数;当x-2<0时即x<2,f(x)=
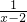 为减函数;
为减函数;故选D.
点评:此题主要考查函数的单调性的判断与证明,此题用类比法,此题是一道基础题.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
 ,则f(x)的定义域为 .
,则f(x)的定义域为 . ,则f(x)( )
,则f(x)( )

 ,则f(x)的值域为 .
,则f(x)的值域为 . ,则f(x)的图象关于( )对称.
,则f(x)的图象关于( )对称. ,则f(x)的单调增区间为 .
,则f(x)的单调增区间为 .