题目内容
设x、y∈R,
、
分别为直角坐标平面内x、y轴正方向上的单位向量,若向量
=x
+(y+2)
,
=x
+(y-2)
,且|
|+|
|=8,求点M(x、y)的轨迹C的方程.
| i |
| j |
| a |
| i |
| j |
| b |
| i |
| j |
| a |
| b |
考点:轨迹方程
专题:计算题,圆锥曲线的定义、性质与方程
分析:先令M(x,y),F1(0,-2),F2(0,2),把|
|+|
|转化为|
|+|
|,再利用|
|+|
|=8即可知道动点M(x,y)的满足椭圆定义,进而求出轨迹C的方程.
| a |
| b |
| F1M |
| F2M |
| a |
| b |
解答:
解:令M(x,y),F1(0,-2),F2(0,2)
则
=
,
=
即|
|+|
|=|
|+|
|
即|
|+|
|=8
又∵|
|=4=2C
∴c=2,a=4,b2=12
所求轨迹方程为
+
=1.
则
| a |
| F1M |
| b |
| F2M |
即|
| a |
| b |
| F1M |
| F2M |
即|
| F1M |
| F2M |
又∵|
. |
| F1F2 |
∴c=2,a=4,b2=12
所求轨迹方程为
| y2 |
| 16 |
| x2 |
| 12 |
点评:本题综合考查了向量垂直问题、轨迹问题,考查学生的计算能力,比较基础.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
我国发射的“嫦娥一号”探月卫星的运行轨道分为三个阶段,绕地阶段、变轨阶段、绕月阶段,绕地阶段时以地球中心F2为焦点的椭圆,近地点A距离地面为m千米,远地点B距离地面为n千米,地球的半径为R千米,则卫星运行轨道的短轴长为( )
A、2
| ||
B、
| ||
| C、mn | ||
| D、2mn |
下列结论中正确的是( )
| A、“x≠1”是“x(x-1)≠0”的充分不必要条件 |
| B、已知随机变量ξ服从正态分布N(5,1),且P(4≤ξ≤6)=0.7,则P(ξ>6)=0.15 |
| C、将一组数据中的每个数据都减去同一个数后,平均数与方差均没有变化 |
| D、某单位有职工750人,其中青年职工350人,中年职工250人,老年职工150人.为了解该单位职工的健康情况,应采用系统抽样的方法从中抽取样本 |
将函数f(x)=sin(x+
)的图象向右平移φ(φ>0)个单位长度,得到的曲线经过原点,则φ的最小值为( )
| π |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
下列四条性质:
①最小正周期是π;
②图象关于直线x=
对称;
③图象关于点(
,0)对称;
④在[-
,
]上是增函数.
下列函数同时具有上述性质的一个函数是( )
①最小正周期是π;
②图象关于直线x=
| π |
| 3 |
③图象关于点(
| π |
| 12 |
④在[-
| π |
| 6 |
| π |
| 3 |
下列函数同时具有上述性质的一个函数是( )
A、y=sin(
| ||||
B、y=sin(2x-
| ||||
C、y=cos(2x+
| ||||
D、y=sin(2x+
|
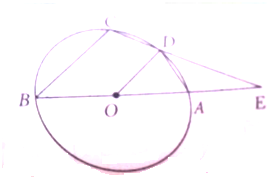 如图,BA是⊙O的直径,延长BA至E,使得AE=AO,过E点作⊙O的割线交⊙O于D、C,使得AD=DC.
如图,BA是⊙O的直径,延长BA至E,使得AE=AO,过E点作⊙O的割线交⊙O于D、C,使得AD=DC.