题目内容
(本题满分12分)设 的定义域为
的定义域为 ,且在
,且在 是递增的,
是递增的,
(1)求证: ;
;
(2)设 ,解不等式
,解不等式 .
.
(1)详见解析;(2)
【解析】
试题分析:(1)赋值法.令 代入条件式,得
代入条件式,得 ;
; ;(2)有条件式可得
;(2)有条件式可得 ,又
,又 ,由(1)可知
,由(1)可知 ,再由函数
,再由函数 为定义域上的增函数,去掉函数符号,列不等式组解得即可.
为定义域上的增函数,去掉函数符号,列不等式组解得即可.
试题解析:(1)证明: ,令
,令 ,则有:
,则有: , 2分
, 2分
 4分
4分
(2)【解析】
∵
 ,
,
∵ ,
,
 等价于:
等价于: 8分
8分
由 定义域为
定义域为 可得
可得 10分
10分
 又
又 在
在 上为增函数,
上为增函数,

又
∴原不等式解集为: 12分
12分
考点:(1)赋值法求函数值;(2)抽象函数中单调性的应用.

练习册系列答案
相关题目
 的最小正周期为( )
的最小正周期为( ) B.
B. C.
C. D.
D.
 为
为 的函数,对任意正实数
的函数,对任意正实数 ,
, ,当
,当 时
时 ,则使得
,则使得 的最小实数
的最小实数 的定义域为
的定义域为 ,则函数
,则函数 的定义域是
的定义域是 C.
C. D.
D.
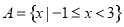 ,
,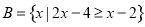 。
。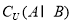 ;
;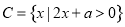 ,满足
,满足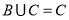 ,求实数
,求实数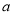 的取值范围。
的取值范围。 是
是 上的增函数,
上的增函数, ,
, 是其图象上的两点,记不等式
是其图象上的两点,记不等式 <
< 的解集
的解集 ,则
,则





 ,则
,则 = .
= .