题目内容
【题目】已知数列![]() 的各项均为正数,前
的各项均为正数,前![]() 项和为
项和为![]() ,首项为2.若
,首项为2.若![]() 对任意的正整数
对任意的正整数![]() ,
,![]() 恒成立.
恒成立.
(1)求![]() ,
,![]() ,
,![]() ;
;
(2)求证:![]() 是等比数列;
是等比数列;
(3)设数列![]() 满足
满足![]() ,若数列
,若数列![]() ,
,![]() ,…,
,…,![]() (
(![]() ,
,![]() )为等差数列,求
)为等差数列,求![]() 的最大值.
的最大值.
【答案】(1)![]() ,
,![]() ,
,![]() ;(2)详见解析;(3)3.
;(2)详见解析;(3)3.
【解析】
(1)由题意利用赋值法,对m,n进行赋值,可得a2,a3,a4;
(2)取m=1,得![]() ,取m=2,得
,取m=2,得![]() .两式相除,得
.两式相除,得![]() ,(n∈N*).结合
,(n∈N*).结合![]() ,可得{Sn+2}是首项为4,公比为2的等比数列,求得
,可得{Sn+2}是首项为4,公比为2的等比数列,求得![]() .进一步求得
.进一步求得![]() .利用定义证得{an}是等比数列;
.利用定义证得{an}是等比数列;
(3)由(2)知,![]() ,设
,设![]() ,
,![]() ,
,![]() 成等差数列,则
成等差数列,则![]() .
.
得到![]() ,分t=r+1和t=r+2两类分析得答案.
,分t=r+1和t=r+2两类分析得答案.
(1)由![]() ,
,![]() 对任意的正整数
对任意的正整数![]() ,
,![]() 恒成立
恒成立
取![]() ,得
,得![]() ,
,
即![]() ,得
,得![]() .
.
取![]() ,
,![]() ,得
,得![]() ,
,
取![]() ,
,![]() ,得
,得![]() ,
,
解得![]() ,
,![]() .
.
(2)取![]() ,得
,得![]() ,
,
取![]() ,得
,得![]() ,
,
两式相除,得,即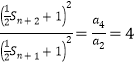 ,即
,即![]()
![]() .
.
由于![]() ,所以
,所以![]() 对任意
对任意![]() 均成立,
均成立,
所以![]() 是首项为4,公比为2的等比数列,
是首项为4,公比为2的等比数列,
所以![]() ,即
,即![]() .
.
![]() 时,
时,![]() ,
,
而![]() 也符合上式,所以
也符合上式,所以![]()
![]() .
.
因为![]() (常数),所以
(常数),所以![]() 是等比数列.
是等比数列.
(3)由(2)知,![]() .
.
设![]() ,
,![]() ,
,![]() 成等差数列,则
成等差数列,则![]() .
.
即![]() ,
,
整理得,![]() .
.
若![]() ,则
,则![]() ,
,
因为![]() ,所以
,所以![]() 只能为2或4,所以
只能为2或4,所以![]() 只能为1或2.
只能为1或2.
若![]() ,则
,则![]() .
.
因为![]() ,故矛盾.
,故矛盾.
综上,只能是![]() ,
,![]() ,
,![]() ,成等差数列或
,成等差数列或![]() ,
,![]() ,
,![]() 成等差数列,其中
成等差数列,其中![]() 为奇数.
为奇数.
所以![]() 的最大值为3.
的最大值为3.

练习册系列答案
相关题目