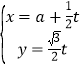题目内容
【题目】选修4-4：坐标系与参数方程
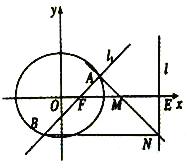
在平面直角坐标系
中，直线
的参数方程为
（
为参数），在以坐标原点为极点，
轴的正半轴为极轴的极坐标系中，曲线
的极坐标方程为
（
且
）.
（I）求直线的极坐标方程及曲线的直角坐标方程；
（Ⅱ）已知
是直线上的一点，
是曲线上的一点， 
，
，若
的最大值为2，求
的值.
【答案】(I) 
；
. (Ⅱ) 
【解析】
（I）利用参数方程、极坐标方程和普通方程互化的公式求直线
的极坐标方程及曲线
的直角坐标方程；（Ⅱ）先利用极坐标方程求出
，
，再求出
，即得
，解之即得a的值.
解：（I）消去参数
，得直线的普通方程为
，
由
，
，
得直线的极坐标方程为
，即.
曲线的极坐标方程为
（
且
），即，
由
，
，得曲线的直角坐标方程为.
（Ⅱ）∵
在直线上，
在曲线上，
∴，，
∴
∴
，.
练习册系列答案
芝麻开花课程新体验系列答案
相关题目
