题目内容
已知函数f(x)的图象向右平移a(a>0)个单位后关于x=a+1对称,当x2>x1>1时,[f(x2)-f(x1)](x2-x1)<0恒成立,设a=f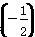 ,b=f(2),c=f(e),则a,b,c的大小关系为( )
,b=f(2),c=f(e),则a,b,c的大小关系为( )
A.c>a>b B.c>b>a
C.a>c>b D.b>a>c
D
[解析] 由题意知,f(x)的图象关于x=1对称,又x2>x1>1时,[f(x2)-f(x1)](x2-x1)<0恒成立,表明函数在(1,+∞)单调递减,所以 ,而e>
,而e> >2>1,所以f(e)<f
>2>1,所以f(e)<f <f(2),即c<a<b,故选D.
<f(2),即c<a<b,故选D.

练习册系列答案
相关题目
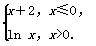 若函数y=|f(x)|-k(x+e2)的零点恰有四个,则实数k的值为( )
若函数y=|f(x)|-k(x+e2)的零点恰有四个,则实数k的值为( )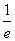

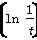 ≤2f(1),那么t的取值范围是________.
≤2f(1),那么t的取值范围是________.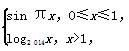
 ,N={y|y=
,N={y|y= +1},则N∩(∁RM)=( )
+1},则N∩(∁RM)=( )